اثبات تطابق قطع مستقيمة

إثبات تطابق القطع المستقيمة

وتستخدم هذه الطريقة لإثبات تطابق القطع المستقيمة غير المتوازية، عن طريق إثبات تطابق مثلثين يتضمنان هاتين القطع المستقيمة.

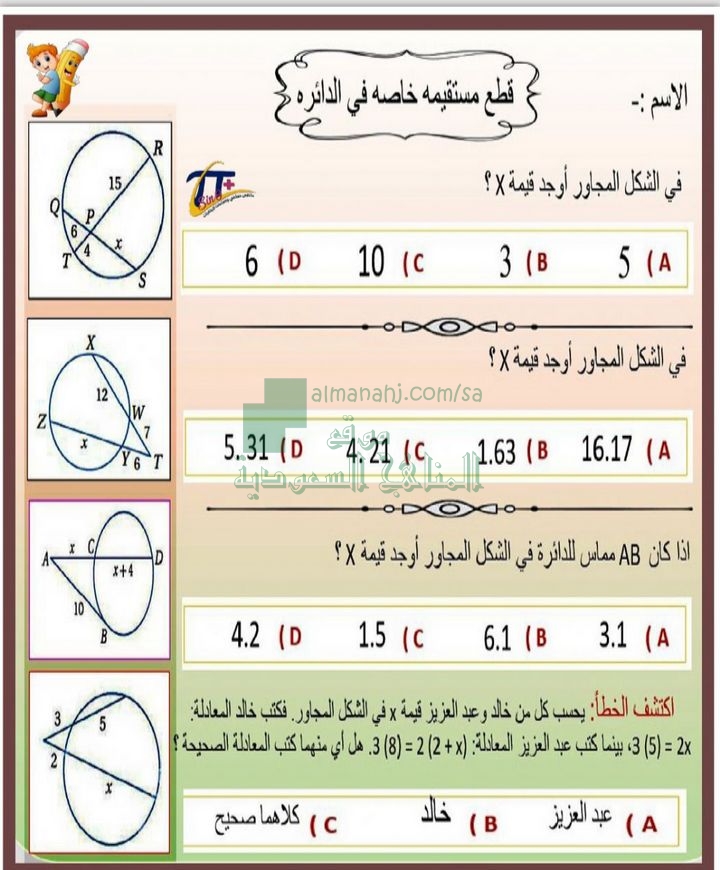
خطوات إثبات تطابق القطع المستقيمة:

1. ارسم قطعة مستقيمة ثالثة تتقاطع مع القطع المستقيمة المطلوب إثبات تطابقهما، لتكوين مثلثين.


2. أثبت تطابق المثلثين باستخدام إحدى حالات تطابق المثلثات المناسبة.

3. إذا كان المثلثان متطابقين، فإن القطع المستقيمة المتناظرة في المثلثين تكون متطابقة أيضًا.

حالات تطابق المثلثات:

حالة ضلع – ضلع – ضلع (س س س): إذا كانت أضلاع المثلثين متطابقة، فإن المثلثين يكونان متطابقين.

حالة ضلع – زاوية – ضلع (س ز س): إذا كان ضلعان وزاوية محصورة بينهما في مثلثين متطابقين، فإن المثلثين يكونان متطابقين.

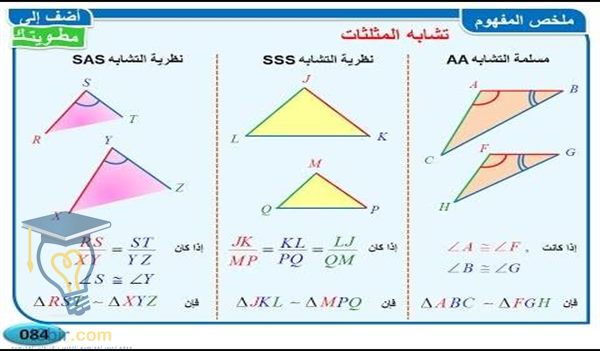
حالة زاوية – ضلع – زاوية (ز س ز): إذا كانت زاويتان وضلع محصور بينهما في مثلثين متطابقين، فإن المثلثين يكونان متطابقين.

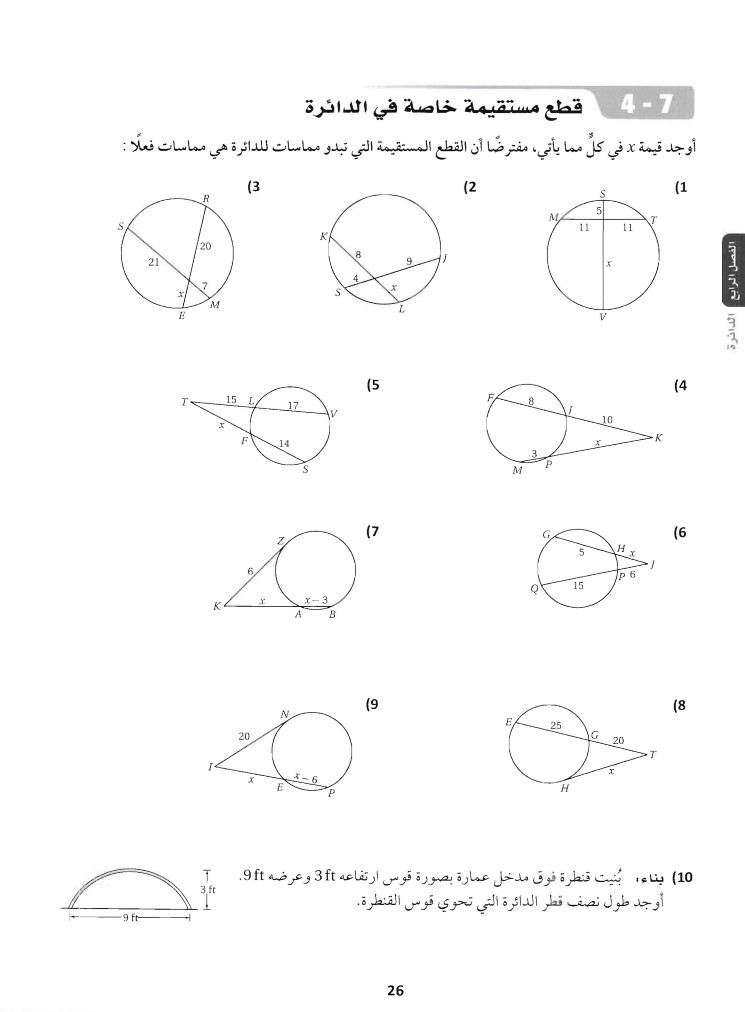
أمثلة على إثبات تطابق القطع المستقيمة:

مثال 1:

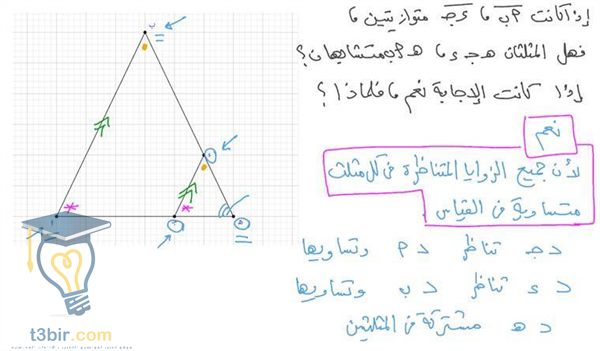
باستخدام حالة ضلع – ضلع – ضلع، يمكن إثبات أن المثلثين متطابقين لأن AE = CE، EF = FD، و AF = CF.

لذلك، فإن القطع المستقيمة المتناظرة في المثلثين متطابقة، مما يعني أن AB = CD.

مثال 2:

باستخدام حالة ضلع – زاوية – ضلع، يمكن إثبات أن المثلثين متطابقين لأن GH = IJ، ∠GKL = ∠IJL، و KL = KL (ضلع مشترك).

لذلك، فإن القطع المستقيمة المتناظرة في المثلثين متطابقة، مما يعني أن GH = IJ.

مثال 3:

باستخدام حالة زاوية – ضلع – زاوية، يمكن إثبات أن المثلثين متطابقين لأن ∠MNS = ∠PQS، NS = QS، و ∠MSN = ∠PSQ.

لذلك، فإن القطع المستقيمة المتناظرة في المثلثين متطابقة، مما يعني أن MN = PQ.

خاتمة:

تُعد طريقة إثبات تطابق القطع المستقيمة باستخدام تطابق المثلثات طريقة شائعة وفعالة في الهندسة لتحديد ما إذا كانت القطع المستقيمة متطابقة أم لا. من خلال إثبات تطابق المثلثات التي تتضمن القطع المستقيمة المعنية، يمكن الاستنتاج أن القطع المستقيمة متطابقة إذا كانت المثلثات متطابقة.