الدوال والمتباينات

الدوال والمتباينات

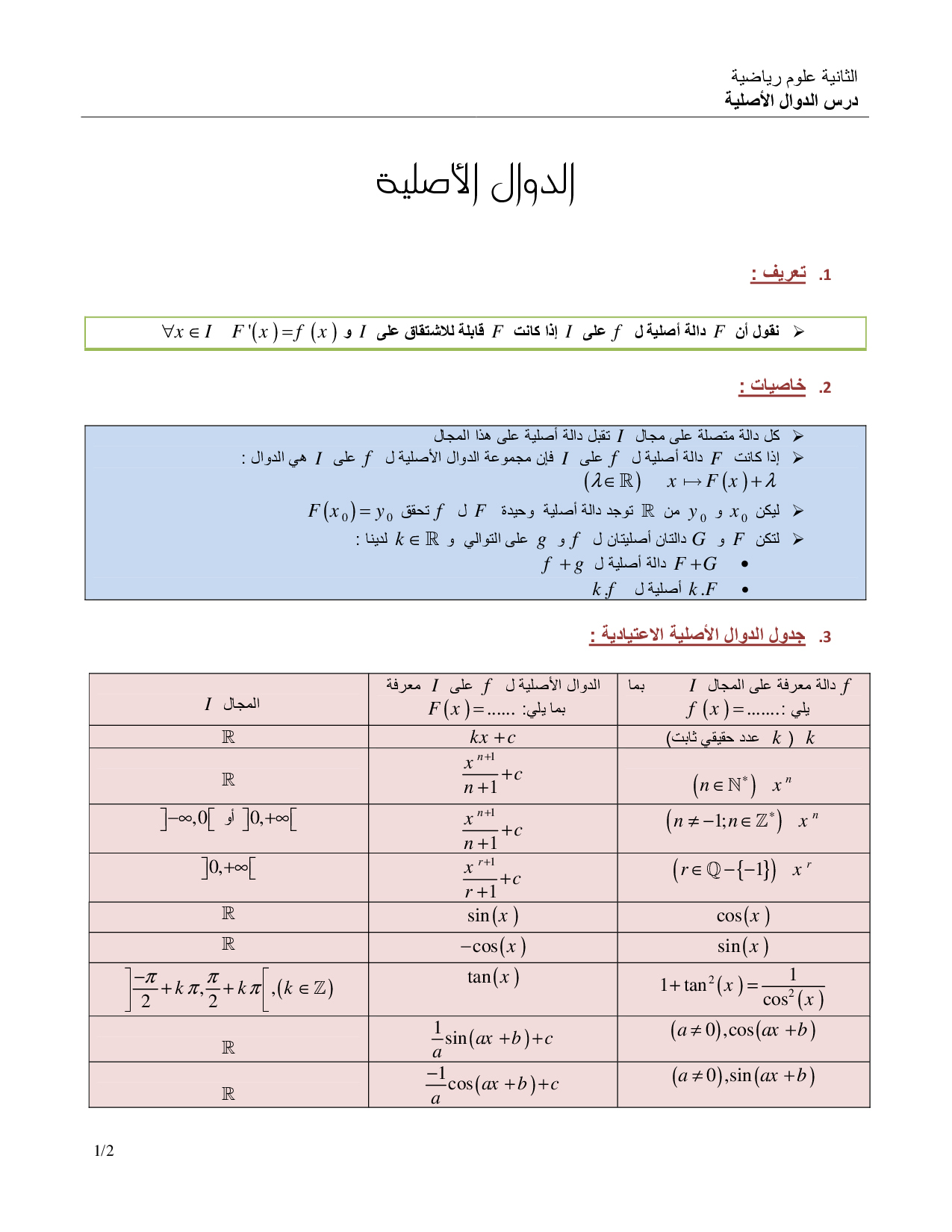
مقدمة

الدوال والمتباينات هما مفهومان أساسيان في الرياضيات لهما تطبيقات واسعة في العديد من المجالات، من علوم الكمبيوتر إلى الفيزياء. الدوال هي قواعد تربط بين متغيرين، بينما المتباينات هي علاقات تربط بين متغيرين.

أنواع الدوال

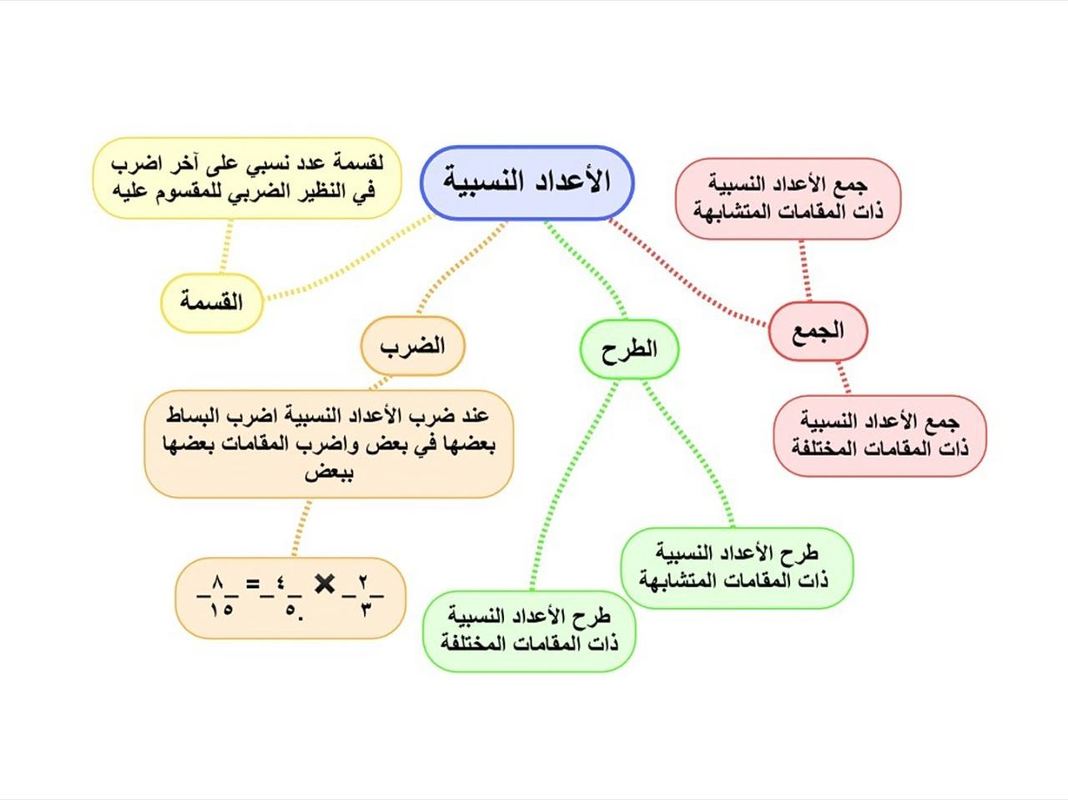
هناك العديد من أنواع الدوال، بما في ذلك:
{|}

* **الدوال الخطية:** هي الدوال التي تكون فيها العلاقة بين المتغيرين خطية، أي يمكن تمثيلها بالمعادلة y = mx + b.
{|}
* **الدوال التربيعية:** هي الدوال التي تكون فيها العلاقة بين المتغيرين تربيعية، أي يمكن تمثيلها بالمعادلة y = ax² + bx + c.

* **الدوال الكسرية:** هي الدوال التي تكون فيها العلاقة بين المتغيرين كسرية، أي يمكن تمثيلها بالمعادلة y = f(x)/g(x).

خصائص الدوال

هناك العديد من الخصائص التي يمكن استخدامها لوصف الدوال، من بينها:

* **المدى:** هو مجموعة جميع القيم التي يمكن أن تأخذها الدالة.

* **المنطقة:** هي مجموعة جميع النقاط (x, y) التي ترضي معادلة الدالة.

* **التزايد/التناقص:** تصف هذه الخاصية ما إذا كانت الدالة تزداد أم تقل عند زيادة المتغير المستقل.

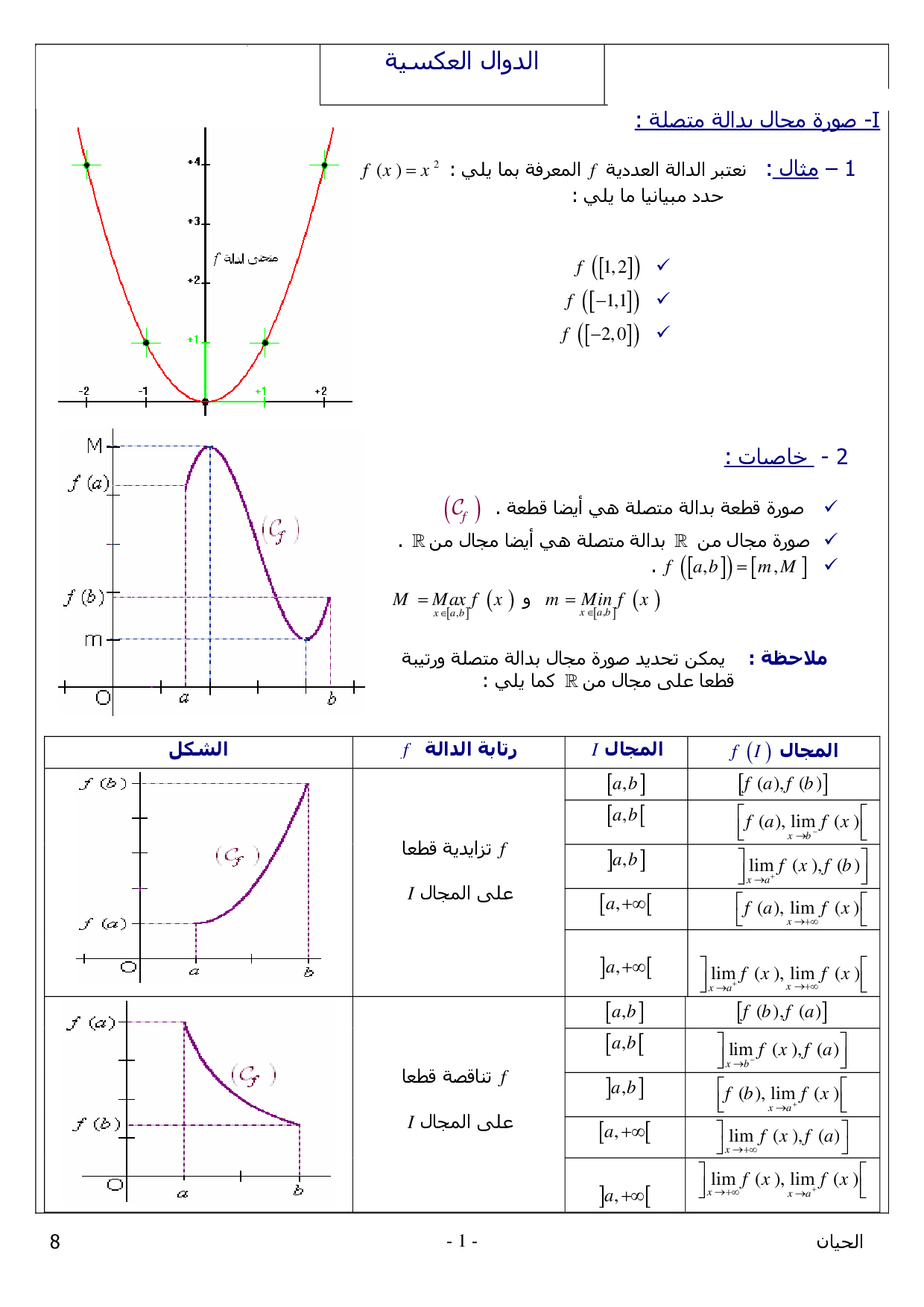
أنواع المتباينات

هناك العديد من أنواع المتباينات، بما في ذلك:

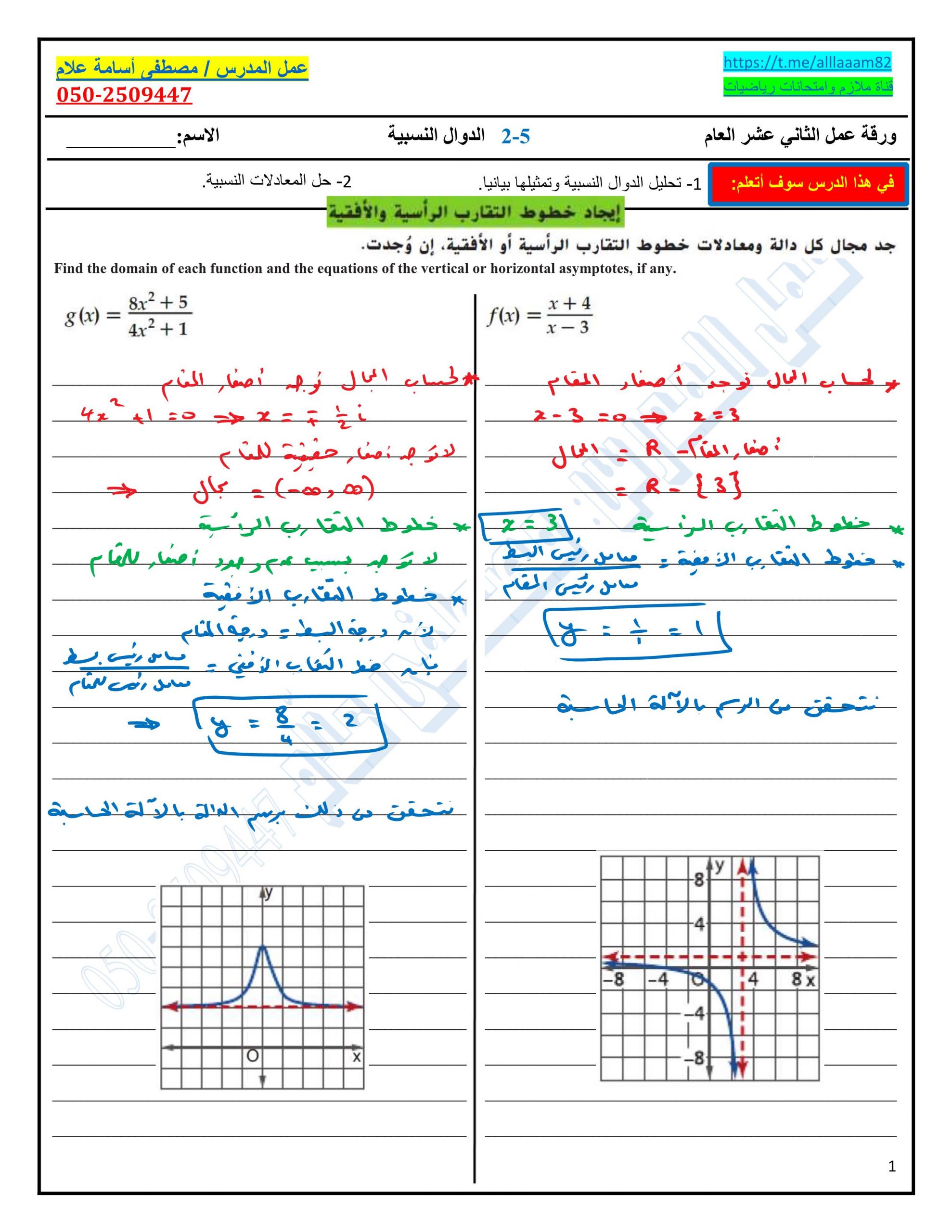
* **المتباينات الخطية:** هي المتباينات التي تكون فيها العلاقة بين المتغيرين خطية، أي يمكن تمثيلها بالمعادلة ax + b > c أو ax + b < c.

* **المتباينات التربيعية:** هي المتباينات التي تكون فيها العلاقة بين المتغيرين تربيعية، أي يمكن تمثيلها بالمعادلة ax² + bx + c > 0 أو ax² + bx + c < 0.

* **المتباينات الكسرية:** هي المتباينات التي تكون فيها العلاقة بين المتغيرين كسرية، أي يمكن تمثيلها بالمعادلة f(x)/g(x) > 0 أو f(x)/g(x) < 0.

خصائص المتباينات

{|}

هناك العديد من الخصائص التي يمكن استخدامها لوصف المتباينات، من بينها:
{|}

* **الحل:** هو قيمة المتغير المستقل التي تجعل المتباينة صحيحة.

* **المجموعة الحل:** هي مجموعة جميع الحلول للمتباينة.

* **التمثيل البياني:** يمكن تمثيل المتباينة بيانياً باستخدام خطوط أو منحنيات غير متقطعة.

تطبيقات الدوال والمتباينات

للدوال والمتباينات تطبيقات واسعة في العديد من المجالات، من بينها:

* **نمذجة العلاقات:** يمكن استخدام الدوال لنمذجة العلاقات بين المتغيرات، مثل العلاقة بين درجة الحرارة والوقت.

* **حل المعادلات:** يمكن استخدام المتباينات لحل المعادلات عن طريق تضييق مجموعة الحلول المحتملة.
* **التحسين:** يمكن استخدام الدوال والمتباينات لإيجاد القيم المثلى للدوال، مثل الحد الأقصى أو الحد الأدنى.
{|}

خاتمة

الدوال والمتباينات هما مفهومان أساسيان في الرياضيات لهما تطبيقات واسعة في العديد من المجالات. من خلال فهم الدوال والمتباينات، يمكننا نمذجة العلاقات وحل المعادلات وإيجاد القيم المثلى.