الصيغة القياسية للكسر العشري واحد واربعون

الصيغة القياسية للكسر العشري هي تمثيل الرقم في صورة رقم صحيح مضروبًا في قوة من عشرة.

القاعدة الأساسية

القاعدة الأساسية لكتابة الكسر العشري في صيغته القياسية هي:

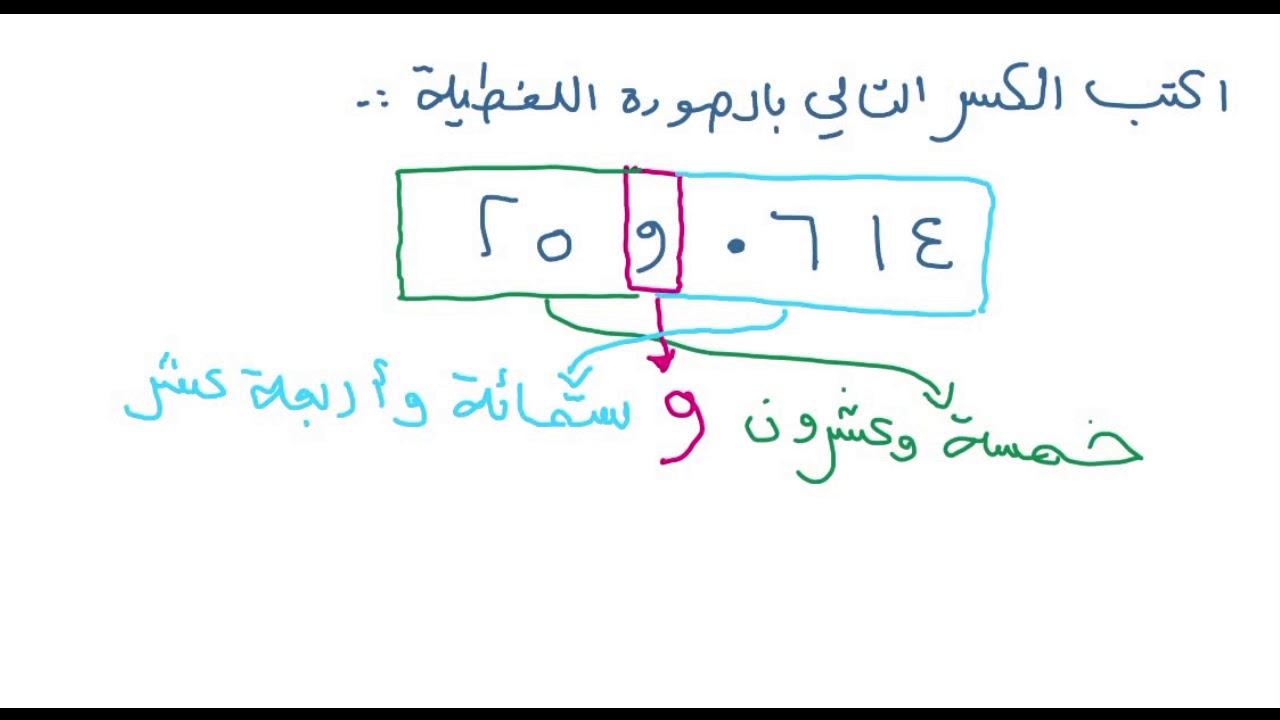
أزل العلامة العشرية وانقل الفاصلة العشرية إلى اليسار بنفس عدد الأرقام بعد العلامة العشرية.

اضرب الرقم الناتج في 10 مرفوعًا إلى قوة عدد الأرقام التي تم نقل الفاصلة العشرية بها.

مثال: الصيغة القياسية لـ 0.41

وفقًا للقاعدة:

أزل العلامة العشرية: 041
انقل الفاصلة العشرية إلى اليسار رقمين: 410

اضرب في 10 مرفوعًا إلى القوة 2: 102 × 410 = 4100

الصيغة القياسية: 4100

تطبيق الصيغة القياسية

تستخدم الصيغة القياسية لحل مجموعة متنوعة من المشكلات، بما في ذلك:
مقارنة الأعداد العشرية
إجراء عمليات حسابية (الجمع والطرح والضرب والقسمة) للأعداد العشرية

تحويل الأعداد العشرية إلى كسور بسيطة
الصيغة القياسية للأعداد العشرية

القاعدة العامة لكتابة أي عدد عشري في صيغته القياسية هي:
أ = (anan-1…a2a1a0.a-1a-2…) 10n

حيث:

A هو العدد العشري في صيغته القياسية
an إلى a0 هي أرقام الجزء الصحيح

a-1 إلى a-n… هي أرقام الجزء العشري

n هو عدد الأرقام بعد العلامة العشرية
أمثلة على الصيغة القياسية
- 0.5 = 10-1 × 5 = 510-1
- 2.34 = 100 × 2 + 10-1 × 3 + 10-2 × 4 = 2100 + 310-1 + 410-2
- 0.0012 = 10-3 × 1 + 10-4 × 2 = 110-3 + 210-4
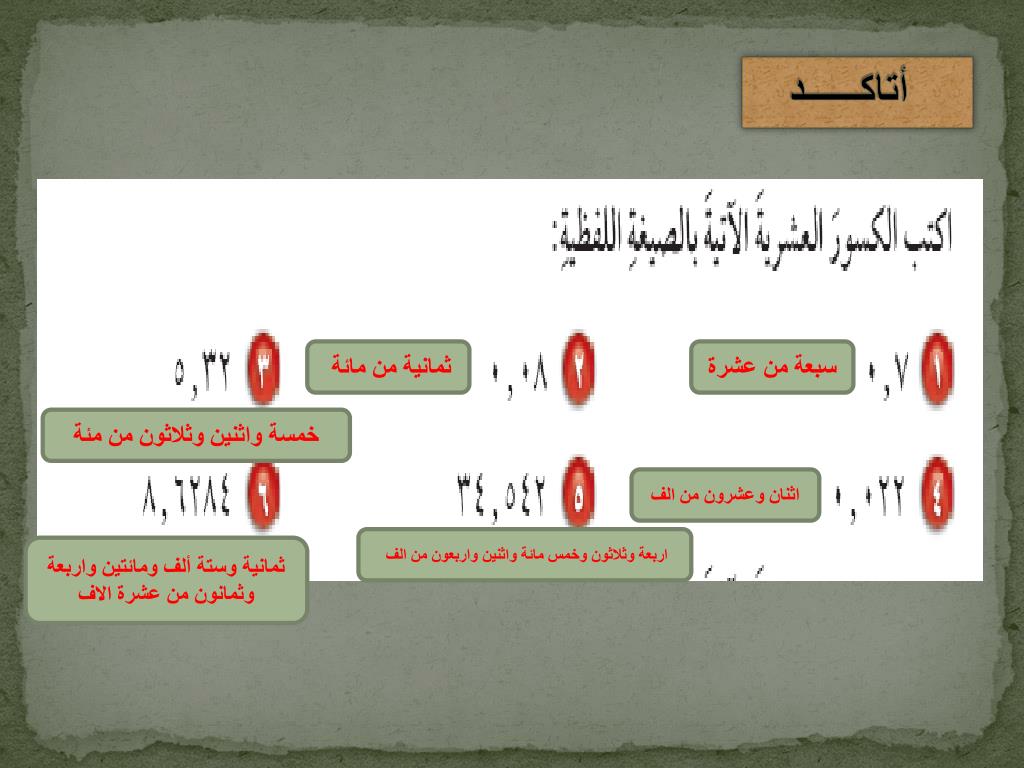
تطبيقات الصيغة القياسية

تستخدم الصيغة القياسية لحل مجموعة متنوعة من المسائل في الرياضيات، مثل:

إيجاد قيمة عدد عشري محدد
مقارنة الأعداد العشرية

تحويل الأعداد العشرية إلى كسور وكسور عشرة

إجراء عمليات حسابية مع الأعداد العشرية
ملاحظات مهمة
من المهم ملاحظة ما يلي عند العمل بالصيغة القياسية للأعداد العشرية:
يمكن تمثيل الأعداد العشرية المنتهية وغير المنتهية وغير الدورية في صيغتها القياسية.

الصيغة القياسية للأعداد العشرية المنتهية لها عدد محدود من الأرقام بعد العلامة العشرية.
الصيغة القياسية للأعداد العشرية غير المنتهية لها عدد لا نهائي من الأرقام بعد العلامة العشرية.

خاتمة

الصيغة القياسية للأعداد العشرية هي تمثيل فريد ومفيد للأعداد العشرية. إنها أداة قوية لحل مجموعة متنوعة من المشكلات في الرياضيات والعلوم والتطبيقات الأخرى.


























