بحث رياضيات أول ثانوي: التبرير والبرهان

التبرير والبرهان هما عمليتان أساسيتان في الرياضيات. التبرير هو عملية تقديم سبب أو دليل لدعم دعوى أو بيان. البرهان هو عملية تقديم سلسلة من الخطوات المنطقية لإثبات أن البيان صحيح. في هذا البحث، سوف نستكشف مفهومي التبرير والبرهان في الرياضيات من خلال مناقشة أنواع مختلفة من التبريرات والبراهين، والخصائص التي تميز كل نوع، وكيفية استخدامها لإثبات صحة العبارات الرياضية.

أنواع التبرير


هناك نوعان رئيسيان من التبرير:
التبرير الاستقرائي يستخدم أمثلة محددة لدعم الدعوى. على سبيل المثال، قد نبرر أن جميع الأعداد الزوجية قابلة للقسمة على 2 عن طريق إظهار أن الأعداد 2 و4 و6 و8 و10 كلها قابلة للقسمة على 2.
التبرير الاستنباطي يستخدم المنطق لإثبات الدعوى. على سبيل المثال، يمكننا أن نبرهن أن مجموع زوايا المثلث يساوي 180 درجة باستخدام مبرهنة مجموع زوايا المثلث.

أنواع البراهين
هناك نوعان رئيسيان من البراهين:
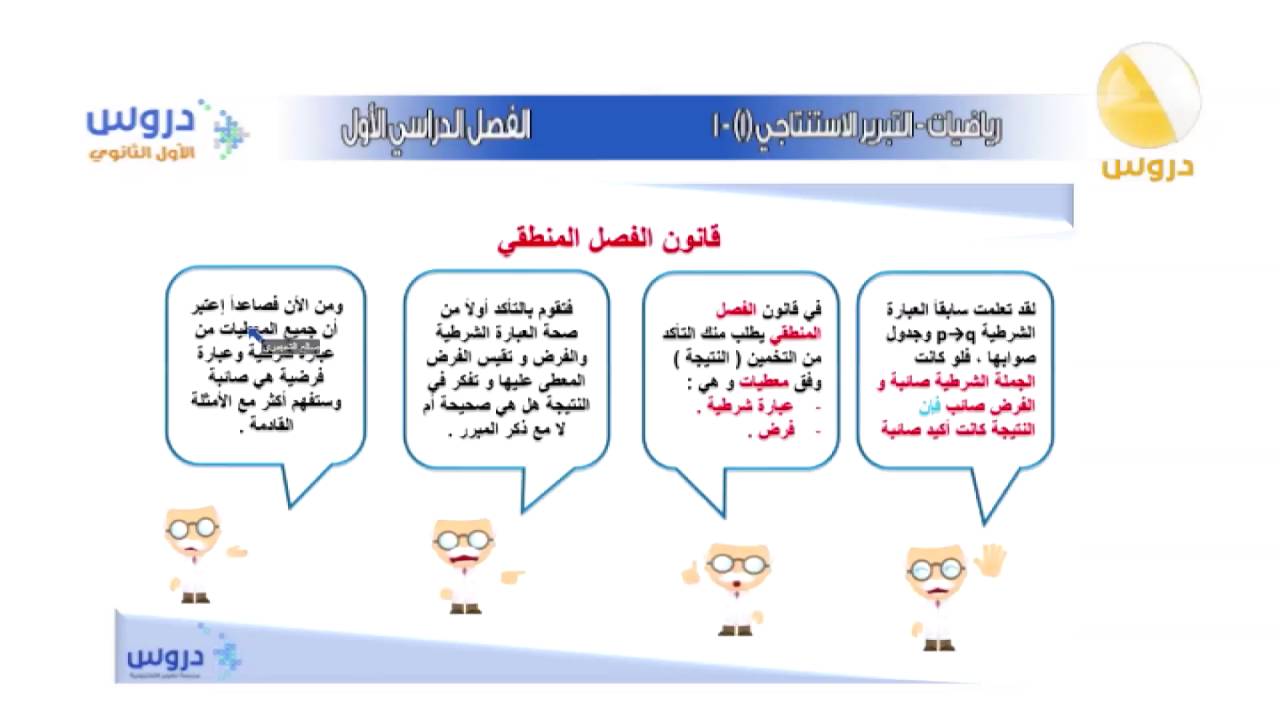
البرهان المباشر يثبت الدعوى باستخدام سلسلة من الخطوات المنطقية. على سبيل المثال، يمكننا إثبات أن مجموع زوايا المستطيل يساوي 360 درجة عن طريق إيجاد قياسات الزوايا الأربع وإظهار أنها مجموعها يساوي 360 درجة.
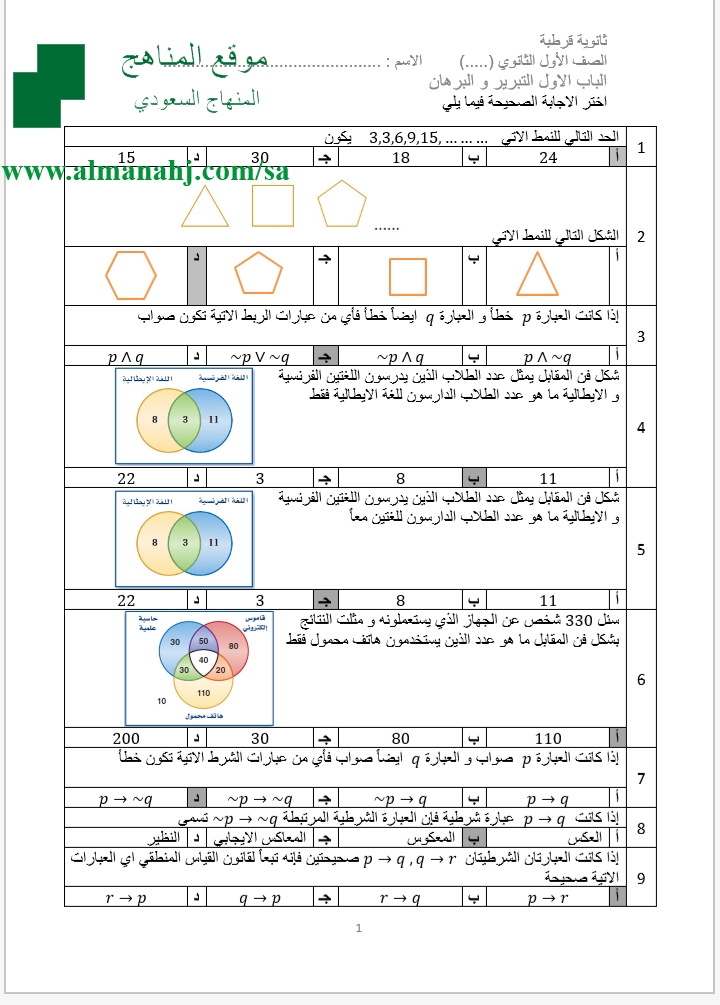
البرهان غير المباشر يثبت الدعوى من خلال إظهار أن نفيها يؤدي إلى تناقض. على سبيل المثال، يمكننا إثبات أن الجذر التربيعي للعدد 2 غير نسبي من خلال إظهار أن افتراض أنه نسبي يؤدي إلى تناقض.
خصائص التبرير والبرهان
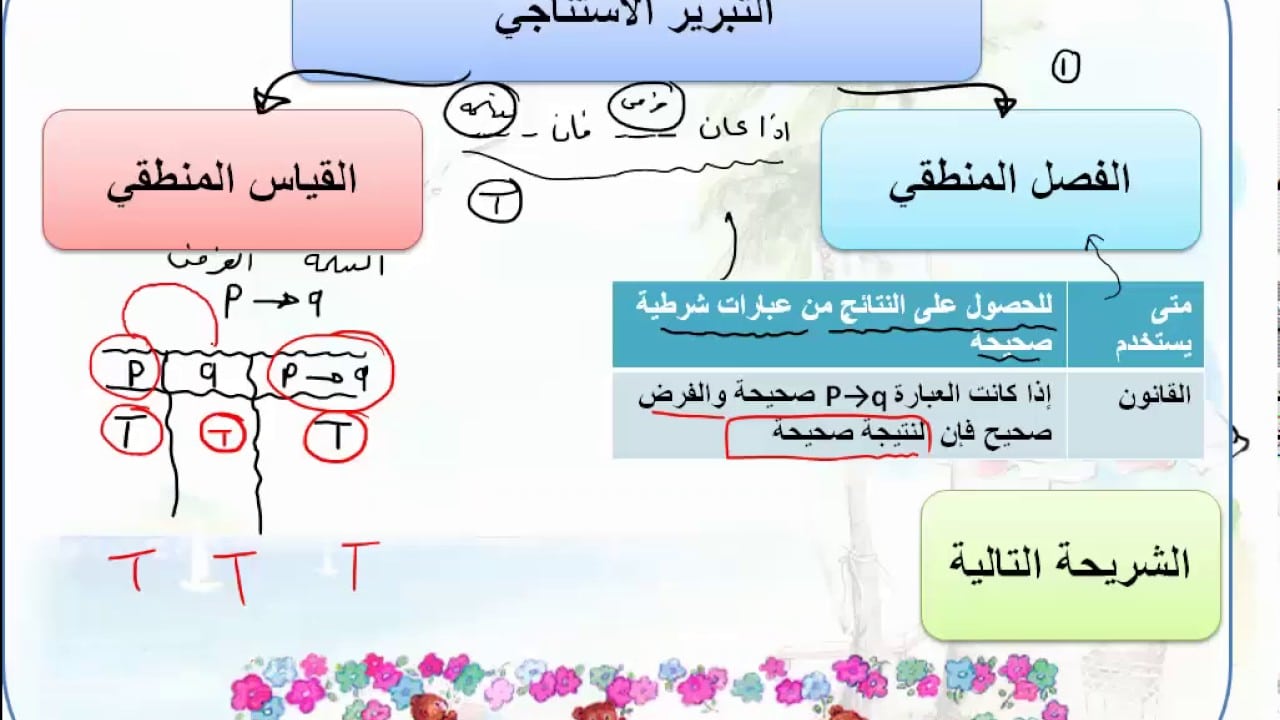
هناك بعض الخصائص التي تميز التبرير والبرهان:

التبرير:
يقدم دعمًا لدعوى أو بيان.
قد لا يكون كافيًا لإثبات صحة الدعوى.
يعتمد على أمثلة محددة أو منطق غير صارم.

البرهان:
يثبت أن دعوى أو بيان صحيح.
هو سلسلة من الخطوات المنطقية.
يستخدم المنطق الصارم والأمثلة العامة.
كيفية استخدام التبرير والبرهان
يمكن استخدام التبرير والبرهان في الرياضيات لإثبات صحة العبارات التالية:

نظريات: هي عبارات عامة يمكن إثباتها من المسلمات باستخدام المنطق.
مبرهنات: هي عبارات يمكن إثباتها باستخدام المنطق من النظريات الأخرى.

لمَّات: هي عبارات مساعدة تُستخدم لإثبات نظريات أو مبرهنات أخرى.

أمثلة على التبرير والبرهان

التبرير: لكي نبرهن أن جميع الأعداد الزوجية أكبر من الصفر، يمكننا تقديم الأمثلة التالية:
2 > 0
4 > 0

6 > 0

…
البرهان: لإثبات أن جميع الأعداد الزوجية أكبر من الصفر، يمكننا استخدام البرهان المباشر التالي:
1. لنفترض أن n عدد زوجي.
2. إذن يوجد عدد صحيح k بحيث n = 2k.
3. بما أن k عدد صحيح، فإن 2k > 0.
4. إذن n = 2k > 0.

التبرير والبرهان هما عمليتان أساسيتان في الرياضيات تُستخدمان لإثبات صحة العبارات الرياضية. التبرير يقدم دعمًا لدعوى أو بيان، بينما البرهان يثبت أن الدعوى أو البيان صحيح. هناك أنواع مختلفة من التبريرات والبراهين ولكل منها خصائصها الخاصة. يمكن استخدام التبرير والبرهان لإثبات صحة النظريات والمبرهنات واللمَّات.