بحث رياضيات ثاني ثانوي العلاقات والدوال

العلاقات والدوال في الرياضيات للصف الثاني الثانوي

العلاقات والدوال هي مفاهيم أساسية في الرياضيات، وتستخدم لوصف العلاقات بين المتغيرات المختلفة. في هذا المقال، سوف نستكشف مفهومي العلاقة والدالة بالتفصيل، ونناقش أنواع مختلفة من العلاقات والدوال وخصائصها.

العلاقات

تعريف العلاقة

العلاقة هي مجموعة من الأزواج المرتبة (x, y) التي تربط المتغير المستقل x بالمتغير التابع y.

أنواع العلاقات

هناك أنواع عديدة من العلاقات، منها:

• العلاقات الخطية: وهي العلاقات التي يمكن تمثيلها بخط مستقيم على المستوى الإحداثي.
• العلاقات غير الخطية: وهي العلاقات التي لا يمكن تمثيلها بخط مستقيم على المستوى الإحداثي.
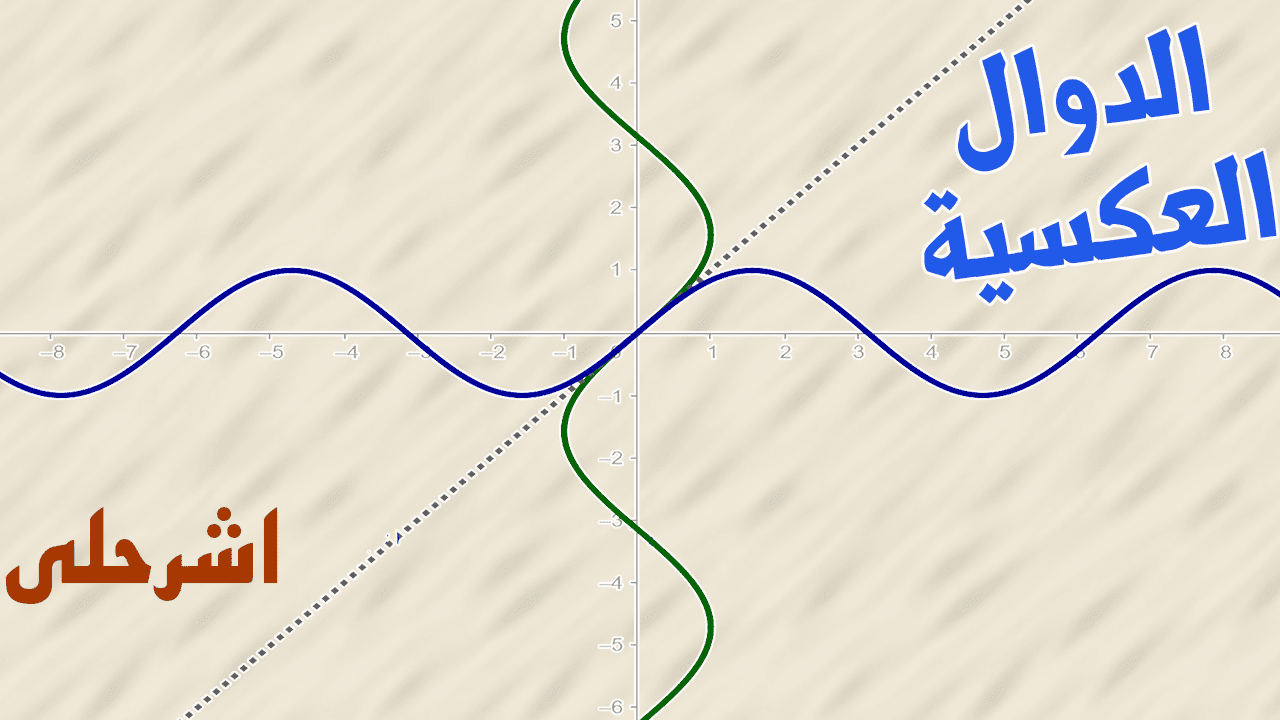
• العلاقات الدورية: وهي العلاقات التي تتكرر فيها قيم المتغير التابع بعد فترات زمنية أو مسافات معينة.

خصائص العلاقات

تتميز العلاقات بعدد من الخصائص، منها:

• المجال: وهو مجموعة جميع قيم المتغير المستقل.
• المدى: وهو مجموعة جميع قيم المتغير التابع.
• الدالة: وهي العلاقة التي لكل قيمة من مجالها تقابلها قيمة وحيدة في مداها.

الدوال

تعريف الدالة

الدالة هي نوع خاص من العلاقات التي لكل قيمة من مجالها تقابلها قيمة وحيدة في مداها.

أنواع الدوال

هناك أنواع عديدة من الدوال، منها:

• الدوال الخطية: وهي الدوال التي يمثلها المعادلة y = mx + b، حيث m هي الميل وb هو الاعتراض.
• الدوال التربيعية: وهي الدوال التي يمثلها المعادلة y = ax² + bx + c، حيث a وb وc ثوابت.
• الدوال الكسرية: وهي الدوال التي يمثلها المعادلة y = f(x)/g(x)، حيث f(x) وg(x) دالتان كثيرات الحدود.

خصائص الدوال

تتميز الدوال بعدد من الخصائص، منها:

• التزايد: وهي الدالة التي تزداد قيمها مع زيادة قيم متغيرها المستقل.
• التناقص: وهي الدالة التي تقل قيمها مع زيادة قيم متغيرها المستقل.
• القيم القصوى والدنيا: وهي أعلى وأدنى قيمة تأخذها الدالة على مجالها.

خصائص الدوال الخاصة

الدالة الخطية

الدالة الخطية هي أبسط أنواع الدوال، وخصائصها هي:

• المجال والمدى: جميع الأعداد الحقيقية.
• التزايد أو التناقص: تتزايد الدالة إذا كان ميلها الموجب وتتناقص إذا كان ميلها السالب.
• القيم القصوى والدنيا: لا يوجد للدالة الخطية قيم قصوى أو دنيا.

الدالة التربيعية

الدالة التربيعية هي دالة من الدرجة الثانية، وخصائصها هي:

• المجال: جميع الأعداد الحقيقية.
• المدى: يعتمد على معامل a، فإذا كان موجبًا فإن المدى هو [a, ∞) وإذا كان سالبًا فإن المدى هو (-∞, a].
• التزايد أو التناقص: تتزايد الدالة التربيعية إذا كان معاملها a موجبًا وتتناقص إذا كان سالبًا.

الدالة الكسرية

الدالة الكسرية هي دالة من الدرجة الأولى، وخصائصها هي:

• المجال: جميع الأعداد الحقيقية ما عدا القيم التي تجعل المقام يساوي الصفر.
• المدى: يعتمد على الدالتين f(x) وg(x)، ولا يمكن تحديده بشكل عام.
• التزايد أو التناقص: يتحدد تزايد أو تناقص الدالة الكسرية من خلال علامة بسطها ومقامها.

استخدامات الدوال

وتستخدام الدوال في العديد من التطبيقات العملية، منها:

• النمذجة: يمكن استخدام الدوال لنمذجة الظواهر الطبيعية والاجتماعية.
• التحليل: يمكن استخدام الدوال لدراسة وتحليل البيانات.
• التنبؤ: يمكن استخدام الدوال للتنبؤ بالقيم المستقبلية بناءً على البيانات السابقة.

العلاقات والدوال هي أدوات رياضية قوية تستخدم لوصف العلاقات بين المتغيرات المختلفة. من خلال دراسة خصائص و أنواع العلاقات والدوال المختلفة، يمكننا اكتساب فهم أعمق للظواهر الطبيعية والاجتماعية والتنبؤ بها.