بحث عن التوابع


1. مفهوم التوابع

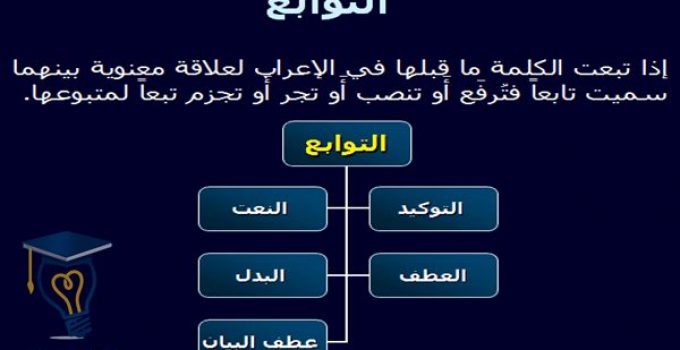


2. تصنيف التوابع

تصنف التوابع إلى أنواع مختلفة بناءً على خصائصها. وتشمل بعض أنواع التوابع الشائعة ما يلي:
• الدوال الخطية: دالة من الدرجة الأولى تمثلها معادلة خطية.

• الدوال التربيعية: دالة من الدرجة الثانية تمثلها معادلة تربيعية.

• الدوال الكسرية: دالة يتم فيها قسمة حاصل جمع على متعدد الحدود.

3. تطبيقات التوابع
تستخدم التوابع على نطاق واسع في العديد من المجالات، بما في ذلك:

• الرياضيات: تستخدم التوابع في الجبر والتحليل وحساب التفاضل والتكامل لحل المعادلات ودراسة الأشكال والأنماط.

• العلوم: تستخدم التوابع في الفيزياء والكيمياء والبيولوجيا لنمذجة الظواهر الطبيعية ووصف العلاقات بين المتغيرات.

• الهندسة: تستخدم التوابع في التصميم والتحليل الهندسي لوصف الأشكال والهياكل وحركة الأجسام.

4. تركيب التوابع
تركيب التوابع هو عملية الجمع بين تابعين لإنشاء تابع جديد. يقوم تابع التركيب بتطبيق تابعًا واحدًا على مخرج تابع آخر.
إذا كان لدينا تابعان f و g، فإن تركيب f بعد g يُكتب على النحو التالي: (f ∘ g)(x) = f(g(x)).
يمكن استخدام تركيب التوابع لإنشاء دوال أكثر تعقيدًا ونمذجة علاقات أكثر تعقيدًا.

5. الدوال العكسية

الدالة العكسية لدالة f هي دالة g بحيث تكون g(f(x)) = x و f(g(x)) = x لجميع قيم x في مجال f ومدى g.
تستخدم الدوال العكسية لحل المعادلات وإيجاد جذور الدوال.

6. اشتقاق التوابع

يتم استخدام الاشتقاق لحساب معدلات التغير، وإيجاد الدوال المتطرفة، ودراسة سلوك الدوال.
يمكن حساب الاشتقاق باستخدام قواعد الاشتقاق أو باستخدام نظرية النهايات.
7. تكامل التوابع
تكامل الدالة هو مجموع مساحات المناطق التي تقع تحت منحنى الدالة. يمثل التكامل مساحة المنطقة أسفل منحنى الدالة فوق محور x.
يتم استخدام التكامل لحساب المساحات والحجوم وأطوال القوس. ويمكن حساب التكامل باستخدام قواعد التكامل أو باستخدام نظرية الأساسية لحساب التفاضل والتكامل.


تعد التوابع أدوات أساسية تستخدم في العديد من التطبيقات في الرياضيات والعلوم والهندسة. وتوفر التوابع وسيلة لنمذجة العلاقات بين المتغيرات ودراسة خصائص الدوال. ومن خلال فهم مفهوم التوابع وتصنيفها وتطبيقاتها وعملياتها، يمكننا استخدام هذه الأدوات القوية لحل المشكلات وتحليل الظواهر.