مقدمة

حل المعادلة هو عملية أساسية في الجبر. تتضمن إيجاد قيمة المتغير الذي يجعل المعادلة صحيحة. يمكن أن تحتوي المعادلات على عمليات مختلفة ومتغيرات متعددة، ويمكن أن تكون خطية أو غير خطية.
أنواع المعادلات
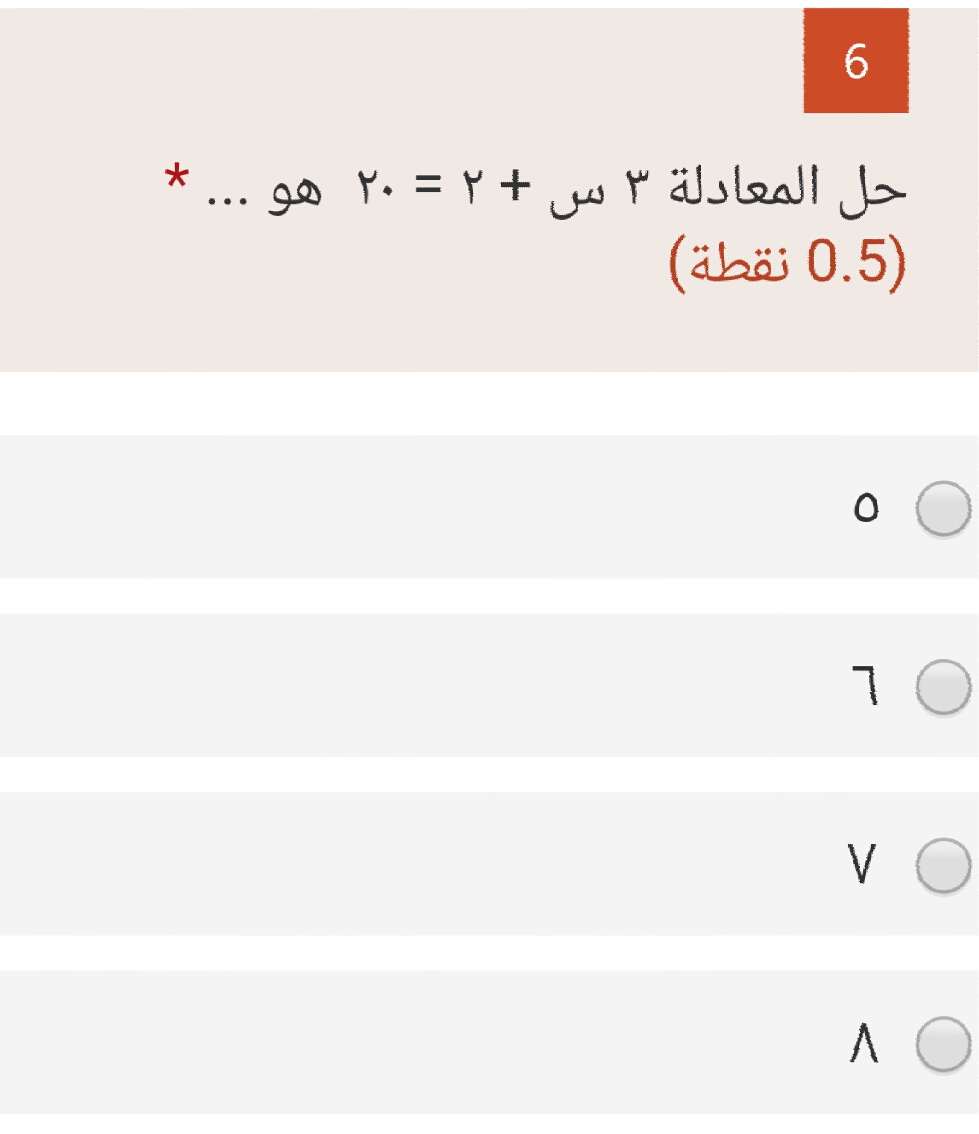
1. معادلات خطية بسيطة
– معادلة تحتوي على متغير واحد وعمليتا الجمع والطرح.

– مثال: 2x + 5 = 11
2. معادلات خطية في متغيرين
– معادلة تحتوي على متغيرين وعمليات الجمع والطرح والضرب.
– مثال: 3x + 2y = 10
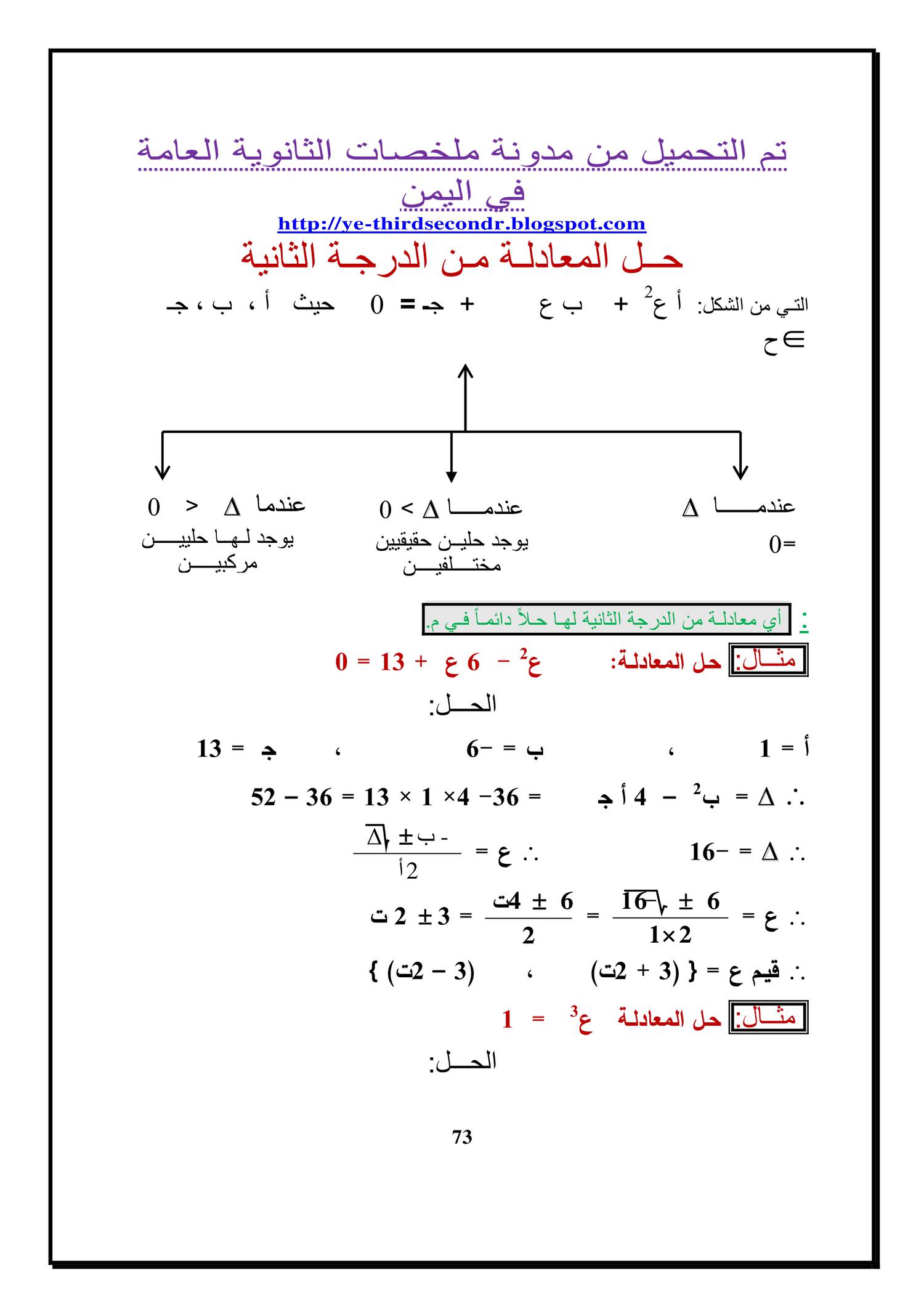
3. معادلات تربيعية
– معادلة تحتوي على متغير واحد مرفوعًا إلى القوة الثانية (x²).

– مثال: x² – 5x + 6 = 0
4. معادلات تكعيبية
– معادلة تحتوي على متغير واحد مرفوعًا إلى القوة الثالثة (x³).
– مثال: x³ + 2x² – 5x + 3 = 0

5. معادلات كسرية

– معادلة تحتوي على كسور.
– مثال: 1/x + 1/2 = 1/4
6. معادلات جذرية
– معادلة تحتوي على جذور تربيعية أو مكعبة وما إلى ذلك.
– مثال: √x + 2 = 5
7. معادلات لوغاريتمية

– معادلة تحتوي على لوغاريتمات.
– مثال: log₂(x) = 3

خطوات حل المعادلة

1. تبسيط المعادلة

– جمع وحذف المصطلحات المتشابهة.

– تحويل الكسور إلى مناظراتها العشرية أو المختزلة.
2. عزل المتغير على جانب واحد من المعادلة
– جمع المتغيرات وطرحها على جانبي المعادلة.
– ضرب وقسمة الأعداد على جانبي المعادلة.
3. حل المتغير

– إجراء العمليات الحسابية المتبقية.

– تحقق من الحل بإعادة استبداله في المعادلة الأصلية.

طرق حل المعادلات
1. طريقة التجميع والطرح
– عزل المتغير الجبري على جانب واحد والعدد على الجانب الآخر.
– إضافة أو طرح نفس العدد إلى كلا جانبي المعادلة.

2. طريقة الضرب والقسمة
– ضرب أو قسمة كلا جانبي المعادلة بنفس العدد.

– تبسيط المعادلة وعزل المتغير.

3. طريقة التعويض
– حل متغير واحد فيما يتعلق بمتغير آخر.

– تعويض التعبير الناتج في معادلة أخرى.

4. طريقة المصفوفات

– استخدام مصفوفة لحل نظام المعادلات الخطية.
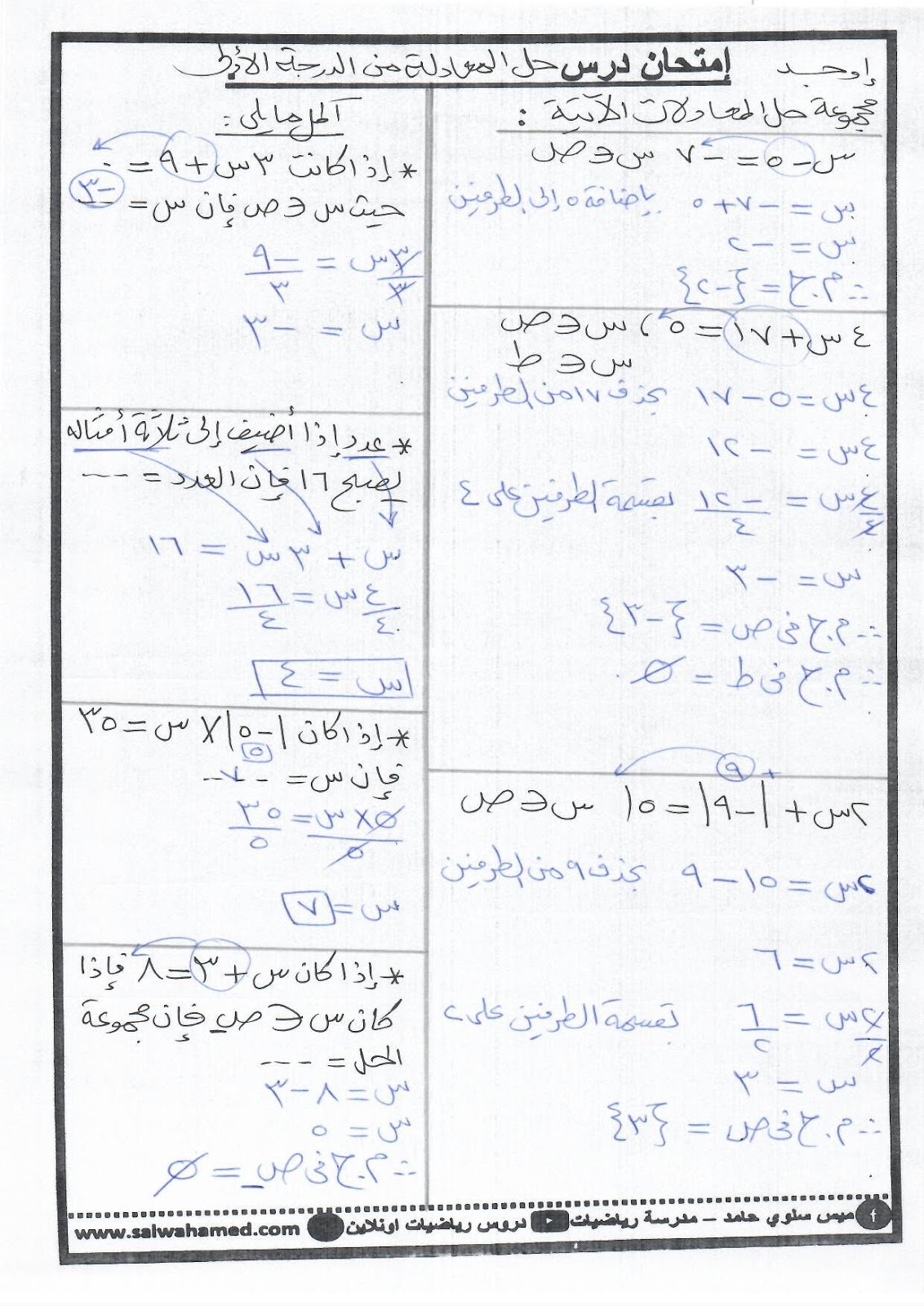
– إيجاد حلول غير محدودة أو لا نهائية أو لا حلول.
5. طريقة الرسم البياني

– رسم البياني لمعادلتين وإيجاد نقطة تقاطعهما.
– الحل هو إحداثيات المتغيرات في نقطة التقاطع.
التطبيقات العملية لحل المعادلات
1. حل المشكلات اللفظية
– ترجمة المشكلة اللفظية إلى معادلة جبرية.
– حل المعادلة لإيجاد المتغير المطلوب.
2. حساب المسافات والسرعات
– استخدام المعادلات لحساب المسافة المقطوعة أو السرعة.
– ربط الوقت والمسافة والسرعة بالمعادلات.
3. حل المعادلات في الفيزياء

– استخدام المعادلات لحل المشكلات المتعلقة بالحركة والقوة والطاقة.
– ربط المتغيرات الفيزيائية بالمعادلات.
أهمية حل المعادلات
1. تطوير مهارات التفكير المنطقي
– تحسين القدرة على تحليل المعلومات وحلها بطريقة منهجية.
– تعزيز الفهم للمفاهيم الجبرية.
2. التطبيقات العملية في مختلف المجالات
– حل المشكلات في العلوم والتكنولوجيا والأعمال.
– صنع القرار واتخاذ الإجراءات بناءً على البيانات والتحليل.

3. أساس للرياضيات المتقدمة
– حل المعادلات هو أساس الجبر والتحليل وغيرها من فروع الرياضيات.
– بناء فهم عميق للرياضيات وتطبيقاتها.
استنتاج
حل المعادلات هو مهارة أساسية في الرياضيات، لها تطبيقات واسعة النطاق في مختلف المجالات. من خلال فهم أنواع المعادلات وطرق حلها، يمكن للمرء تطوير مهارات التفكير المنطقي واتخاذ القرارات المستنيرة. إن إتقان حل المعادلات يوفر أساسًا متينًا للنمو الأكاديمي والمهني.