مقدمة

الأشكال الرباعية هي متعددات الأضلاع ذات أربع أضلاع وأربع زوايا. وهي من أكثر الأشكال الهندسية شيوعًا في الطبيعة والهندسة المعمارية والتصميم. وتتميز هذه الأشكال بمجموعة متنوعة من الخصائص التي تحدد أشكالها وصفاتها.
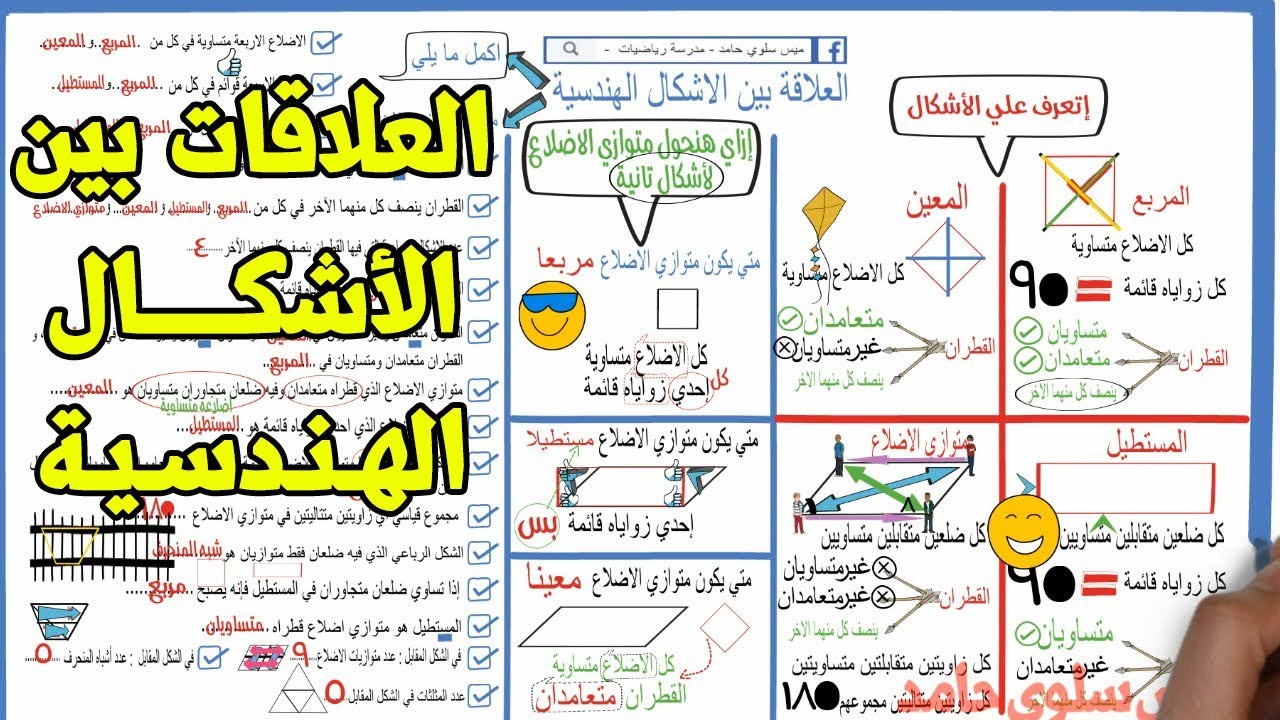
خصائص الأشكال الرباعية
1. الأضلاع والزوايا


تتكون الأشكال الرباعية من أربع أضلاع متصلة بأربع زوايا. ويبلغ مجموع زوايا أي شكل رباعي دائمًا 360 درجة.

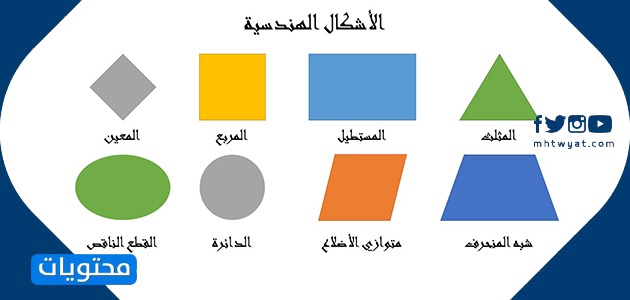
يُصنف وفقًا للأضلاع التالية:

- متوازي الأضلاع: أضلاع متقابلة متوازية ومستقيمة.
- شبه منحرف: ضلعان متوازيان فقط.
- معين: أضلاع متساوية وزوايا متقابلة متساوية.
- مستطيل: زوايا قائمة.
- مربع: أضلاع متساوية وزوايا قائمة.
2. القطر

القطر هو قطعة مستقيمة تربط بين نقطتين غير متجاورتين على الشكل. ويقسم القطر الشكل إلى مثلثين متطابقين.

3. المحور:

المحور هو خط مستقيم يربط بين منتصف الضلعين المتقابلين. وينصف المحور الشكل إلى مثلثين متطابقين أيضًا.
4. الأقطار المتعامدة:

في بعض الأشكال الرباعية، مثل المستطيل والمربع، تتقاطع الأقطار عند نقطة واحدة وتكون متعامدة عليها.

5. الزوايا المتقابلة:

في متوازي الأضلاع، تكون الزوايا المتقابلة متساوية. وفي المستطيل والمربع، تكون الزوايا المتقابلة متساوية وقائمة.

6. الأضلاع المتقابلة:

في متوازي الأضلاع، تكون الأضلاع المتقابلة متساوية. وفي المستطيل والمربع، تكون جميع الأضلاع متساوية.

7. المساحة:

تُحسب مساحة الأشكال الرباعية باستخدام الصيغة المناسبة لنوع الشكل. على سبيل المثال، تُحسب مساحة المستطيل بضرب الطول في العرض.

الخاتمة
للأشكال الرباعية خصائص متعددة تحدد أشكالها وصفاتها. ومن خلال فهم هذه الخصائص، يمكننا تحليل وتصنيف الأشكال الرباعية المختلفة بشكل فعال. وتُستخدم الأشكال الرباعية على نطاق واسع في العديد من التطبيقات العملية، بما في ذلك الهندسة المعمارية، والتصميم، والرياضيات.
