الدوال الخاصة في الرياضيات للصف الثاني الثانوي

مقدمة
الدوال الخاصة هي فئة مهمة من الدوال لها خصائص وتطبيقات مميزة في مجالات مختلفة من الرياضيات والعلوم والتكنولوجيا. وفي هذا المقال، سنستكشف بعضًا من أشهر الدوال الخاصة المستخدمة في الصف الثاني الثانوي.

الدالة الخطية

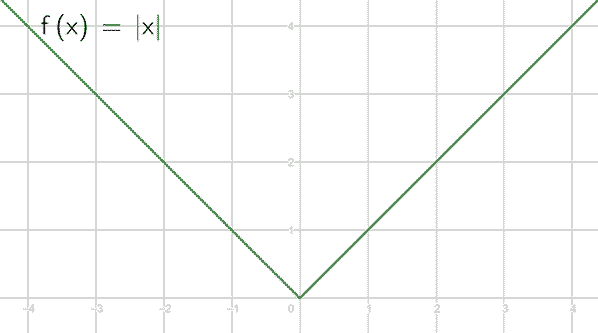
هي دالة من الشكل f(x) = mx + b حيث m و b ثابتان. والدالة الخطية هي دالة بسيطة ولها مخطط بياني خطي.

مثال 1: الدالة f(x) = 2x + 3 هي دالة خطية، ومخططها البياني هو خط ميله 2 ويقطع محور y عند النقطة (0، 3).

مثال 2: الدالة g(x) = -x + 5 هي دالة خطية، ومخططها البياني هو خط ميله -1 ويقطع محور y عند النقطة (0، 5).

الدالة التربيعية
هي دالة من الشكل f(x) = ax² + bx + c حيث a و b و c ثابتات. والدالة التربيعية هي دالة من الدرجة الثانية، ومخططها البياني هو قطع مكافئ.

مثال 1: الدالة f(x) = x² – 2x + 1 هي دالة تربيعية، ومخططها البياني هو قطع مكافئ له قمة عند النقطة (1، 0).

مثال 2: الدالة g(x) = -x² + 3x – 5 هي دالة تربيعية، ومخططها البياني هو قطع مكافئ له قمة عند النقطة (3/2، -11/4).
الدالة المتعددة الحدود
هي دالة من الشكل f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + … + a₁x + a₀ حيث a₀ و a₁ و … و aₙ ثابتات. والدالة المتعددة الحدود هي دالة من الدرجة n، ومخططها البياني يتكون من مجموعة من القطع المكافئة.

مثال 1: الدالة f(x) = x³ – 2x² + x – 3 هي دالة متعددة الحدود من الدرجة الثالثة، ومخططها البياني يتكون من ثلاثة قطع مكافئة.

مثال 2: الدالة g(x) = -2x⁴ + 5x² – 1 هي دالة متعددة الحدود من الدرجة الرابعة، ومخططها البياني يتكون من أربعة قطع مكافئة.
الدالة الكسرية
هي دالة من الشكل f(x) = p(x) / q(x) حيث p(x) و q(x) متعددتان حدوديتان و q(x) ≠ 0. والدالة الكسرية هي دالة غير معرفة عند القيم التي تجعل مخرجها (القاسم) يساوي الصفر.

مثال 1: الدالة f(x) = (x – 1) / (x + 2) هي دالة كسرية، وهي غير معرفة عند x = -2.
مثال 2: الدالة g(x) = x² / (x² – 4) هي دالة كسرية، وهي غير معرفة عند x = -2 و x = 2.

الدالة الجذرية

هي دالة من الشكل f(x) = √(x) حيث x ≥ 0. والدالة الجذرية هي دالة معرفة عند القيم غير السالبة (التي تساوي الصفر أو أكبر من الصفر)، ومخططها البياني يتكون من جزء مكافئ متزايد.
مثال 1: الدالة f(x) = √(x) هي دالة جذرية، ومخططها البياني هو جزء مكافئ متزايد يبدأ من النقطة (0، 0).

مثال 2: الدالة g(x) = √(x – 2) هي دالة جذرية، ومخططها البياني هو جزء مكافئ متزايد يبدأ من النقطة (2، 0).
الدالة الأسية

هي دالة من الشكل f(x) = aˣ حيث a عدد حقيقي موجب مختلف عن 1. والدالة الأسية هي دالة معرفة عند جميع القيم الحقيقية، ومخططها البياني يتكون من منحنى يتزايد بشكل سريع للأسس الموجبة وينقص بشكل سريع للأسس السالبة.

مثال 1: الدالة f(x) = 2ˣ هي دالة أسية، ومخططها البياني هو منحنى متزايد يبدأ من النقطة (0، 1).
مثال 2: الدالة g(x) = (1/2)ˣ هي دالة أسية، ومخططها البياني هو منحنى متزايد يبدأ من النقطة (0، 1).

الدالة اللوغاريتمية
هي دالة من الشكل f(x) = logₐ(x) حيث a عدد حقيقي موجب مختلف عن 1. والدالة اللوغاريتمية هي دالة معرفة عند القيم الموجبة، ومخططها البياني يتكون من منحنى يتزايد ببطء.

مثال 1: الدالة f(x) = log₂(x) هي دالة لوغاريتمية، ومخططها البياني هو منحنى متزايد يبدأ من النقطة (1، 0).

مثال 2: الدالة g(x) = log₅(x) هي دالة لوغاريتمية، ومخططها البياني هو منحنى متزايد يبدأ من النقطة (1، 0).

خاتمة
تُستخدم الدوال الخاصة بشكل واسع في مجالات مختلفة من الرياضيات والعلوم والتكنولوجيا. من خلال فهم هذه الدوال وخصائصها، يمكن للطلاب تحليل الدوال المتعلقة بها وحلها والتنبؤ بسلوكها.