الدوال الخاصة في الرياضيات للصف الثاني الثانوي
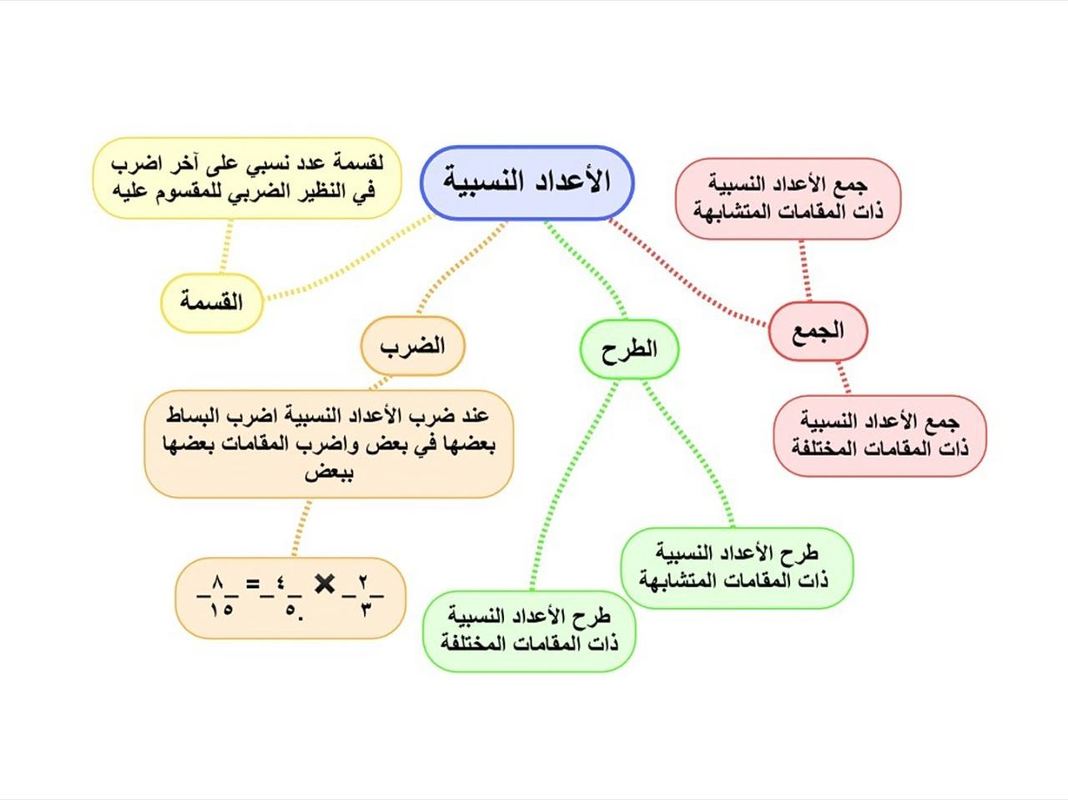
الدوال الخاصة هي دوال رياضية لها خصائص مميزة تميزها عن غيرها من الدوال، وتُستخدم في العديد من المجالات العلمية والهندسية والتطبيقية، وفي هذا المقال، سنتناول أهم الدوال الخاصة التي يتم دراستها في الصف الثاني الثانوي، مع ذكر أمثلة توضيحية على كل منها.

الدالة الأسية

الدالة الأسية هي دالة من الشكل y = a^x، حيث a عدد حقيقي موجب غير 1، وx هو المتغير المستقل. وهي دالة متزايدة إذا كان a > 1 ومتناقصة إذا كان a < 1.

مثال 1: y = 2^x هي دالة أسية متزايدة حيث a = 2 > 1.
مثال 2: y = (1/2)^x هي دالة أسية متناقصة حيث a = 1/2 < 1.
مثال 3: الدالة الأسية e^x هي إحدى أهم الدوال الخاصة وتُستخدم في العديد من التطبيقات، مثل حساب الفائدة المركبة.
الدالة اللوغاريتمية

الدالة اللوغاريتمية هي دالة من الشكل y = logax، حيث a عدد حقيقي موجب غير 1، وx هو المتغير المستقل. وهي الدالة العكسية للدالة الأسية، أي logax = y إذا وفقط إذا a^y = x.

مثال 1: y = log2x هي دالة لوغاريتمية حيث a = 2.
مثال 2: y = log10x هي دالة لوغاريتمية حيث a = 10.

مثال 3: الدالة اللوغاريتمية الطبيعية lnx تُستخدم على نطاق واسع في حساب التفاضل والتكامل والتطبيقات الأخرى.

الدالة المثلثية
الدوال المثلثية هي دوال تُستخدم لدراسة زوايا المثلثات، وتشمل هذه الدوال:
جيب الزاوية: sinx

جيب التمام: cosx
الظل: tanx

القاطع: cscx

القاطع التمام: secx
الظل التمام: cotx

مثال 1: sin30 = 1/2 هي قيمة جيب زاوية 30 درجة.
مثال 2: cos60 = 1/2 هي قيمة جيب تمام زاوية 60 درجة.
مثال 3: tan45 = 1 هي قيمة ظل زاوية 45 درجة.
الدالة المثلثية العكسية

الدوال المثلثية العكسية هي الدوال العكسية للدوال المثلثية، وتُستخدم لحساب قيمة الزاوية التي يتطابق فيها قيمتها الجيبية أو جيب تمامها أو ظلها مع قيمة معينة.
مثال 1: arcsin(1/2) = 30 درجة هي الزاوية التي يتطابق فيها جيبها مع 1/2.

مثال 2: arccos(1/2) = 60 درجة هي الزاوية التي يتطابق فيها جيب تمامها مع 1/2.

مثال 3: arctan(1) = 45 درجة هي الزاوية التي يتطابق فيها ظلها مع 1.
الدالة الأسية المتعددة الحدود
الدالة الأسية المتعددة الحدود هي دالة من الشكل y = a0 + a1x + a2x^2 + … + anx^n، حيث a0, a1, …, an أعداد حقيقية وx هو المتغير المستقل. وهي دالة متعددة الحدود يتم رفعها إلى الأس.

مثال 1: y = (x + 1)^2 هي دالة أسية متعددة الحدود حيث n = 2.
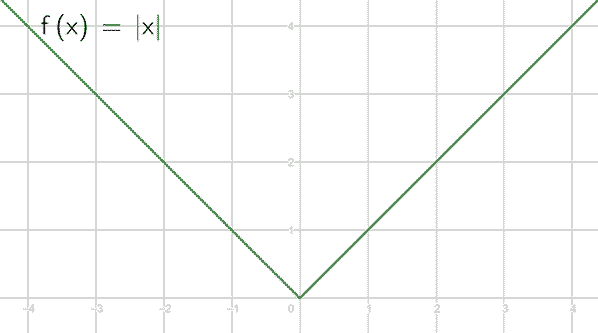
مثال 2: y = (x – 2)^3 هي دالة أسية متعددة الحدود حيث n = 3.

مثال 3: الدالة الأسية المتعددة الحدود e^x هي حالة خاصة من الدالة الأسية حيث a0 = 1 وa1 = 1 وجميع المعاملات الأخرى تساوي الصفر.

الدالة الكسرية
الدالة الكسرية هي دالة من الشكل y = f(x)/g(x)، حيث f(x) وg(x) متعددتان الحدود. وتُستخدم لدراسة السلوك غير المنتظم للدوال، مثل ما يحدث عندما يكون المقام يساوي الصفر.

مثال 1: y = x/(x-1) هي دالة كسرية غير معرفة عند x = 1.

مثال 2: y = (x^2 – 1)/(x – 1) هي دالة كسرية يمكن تبسيطها إلى y = x + 1.
مثال 3: الدالة الكسرية 1/x تُستخدم على نطاق واسع في حساب التفاضل والتكامل والتطبيقات الأخرى.
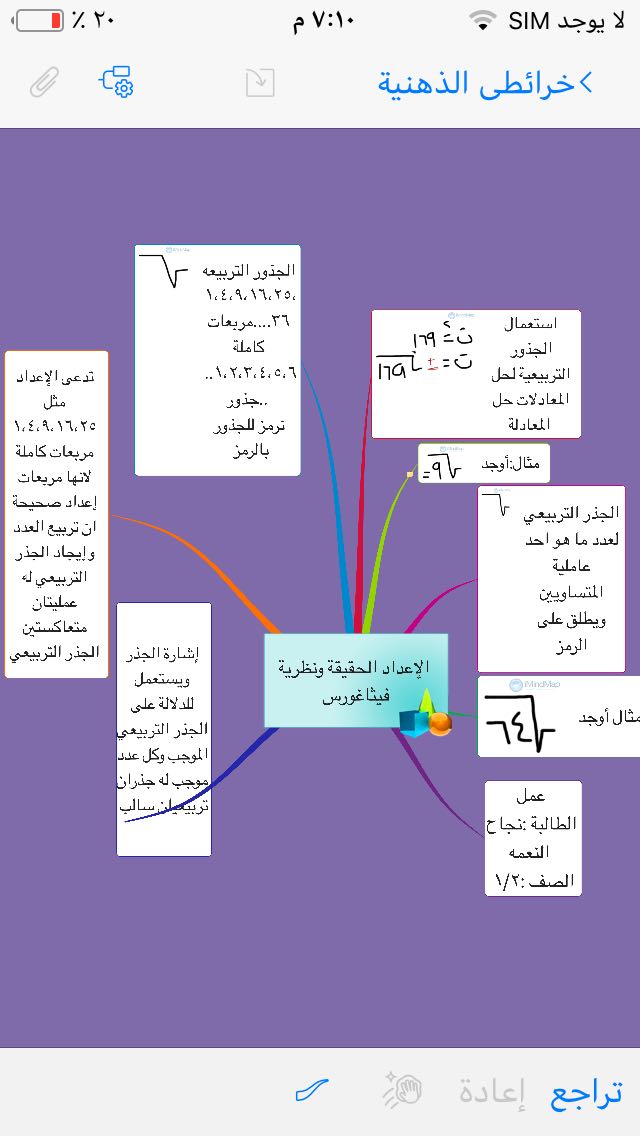
الدالة الجذرية

الدالة الجذرية هي دالة من الشكل y = n√x، حيث n عدد صحيح موجب يسمى مؤشر الجذر وx هو المتغير المستقل. وتُستخدم لحساب الجذور النونية للأعداد.
مثال 1: y = √x هي دالة جذرية حيث n = 2.
مثال 2: y = 3√x هي دالة جذرية حيث n = 3.
مثال 3: الدالة الجذرية n√x تُستخدم على نطاق واسع في حساب التفاضل والتكامل والتطبيقات الأخرى.
الخاتمة
إن الدوال الخاصة هي أدوات رياضية قوية تُستخدم في العديد من المجالات العلمية والهندسية والتطبيقية. وفي هذا المقال، قمنا باستكشاف أهم الدوال الخاصة التي يتم دراستها في الصف الثاني الثانوي، مع ذكر أمثلة توضيحية على كل منها. ومن خلال فهم هذه الدوال، يمكن للطلاب توسيع معرفتهم بالرياضيات وتطوير مهاراتهم في حل المشكلات.