مطوية الضرب

مقدمة مطوية الضرب

مفهوم الضرب هو عملية الجمع المتكررة لعدد معين، والناتج النهائي يُعرف باسم الجداء، وفي الرياضيات، يتم استخدام عملية الضرب للإيجاد مساحة المستطيل، وإيجاد المسافة المقطوعة، وإيجاد أي قيمة غير معروفة في المعادلة، وفيما يلي سنتعرف على مزيد من المعلومات حول الضرب وطرق حله.

خصائص الضرب


- التبديلية: يمكن تبديل ترتيب العوامل دون تغيير الناتج، أي 3 × 5 = 5 × 3
- التجميعية: يمكن تجميع العوامل في أقواس دون تغيير الناتج، أي (2 × 3) × 4 = 2 × (3 × 4)
- التوزيعية: يمكن ضرب مجموع أو طرح عددين في عدد ثالث، عن طريق ضرب كل عدد فردي في العدد الثالث ثم جمع أو طرح النتائج، أي 3 × (4 + 5) = 3 × 4 + 3 × 5
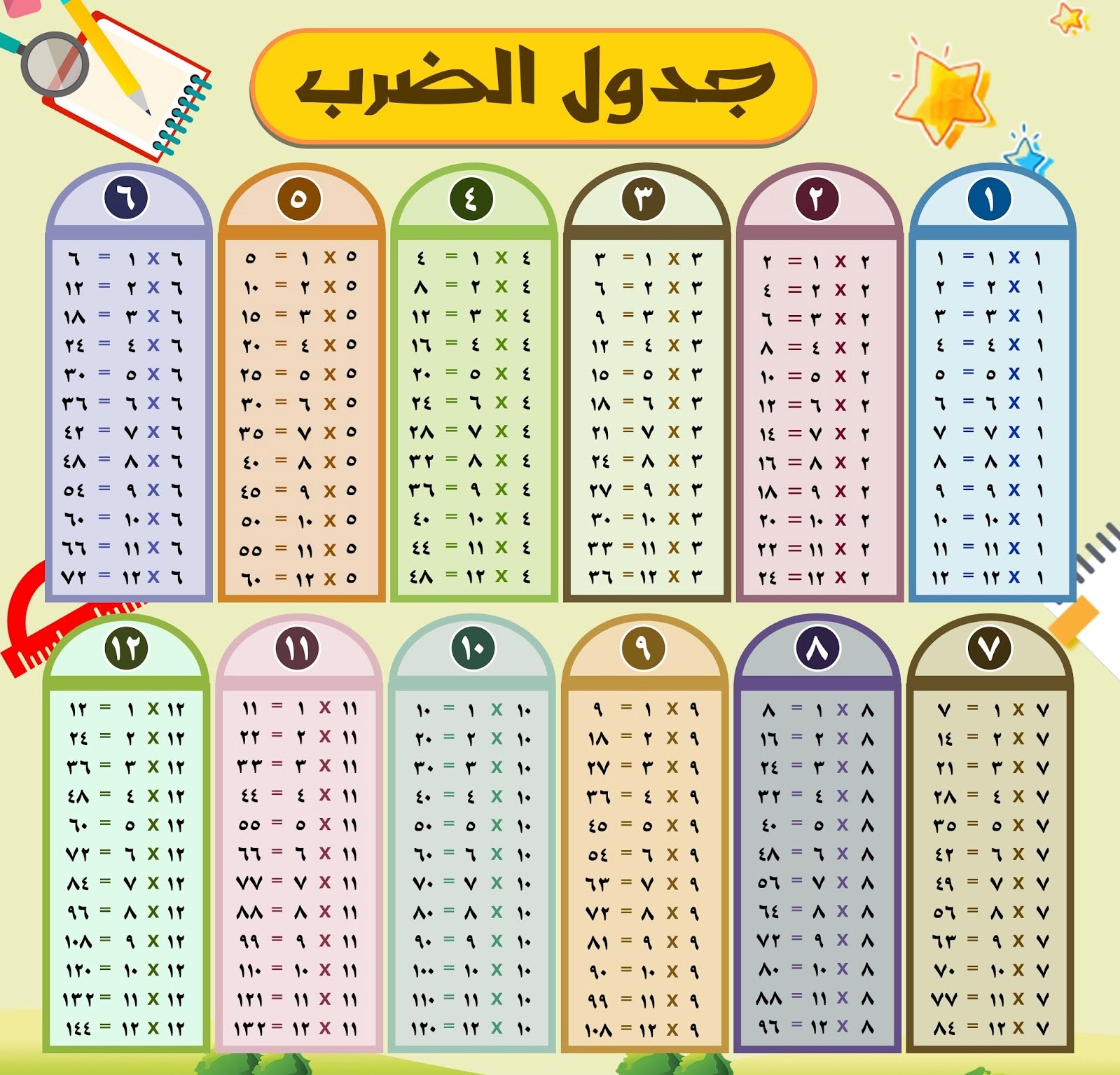
طرق الضرب
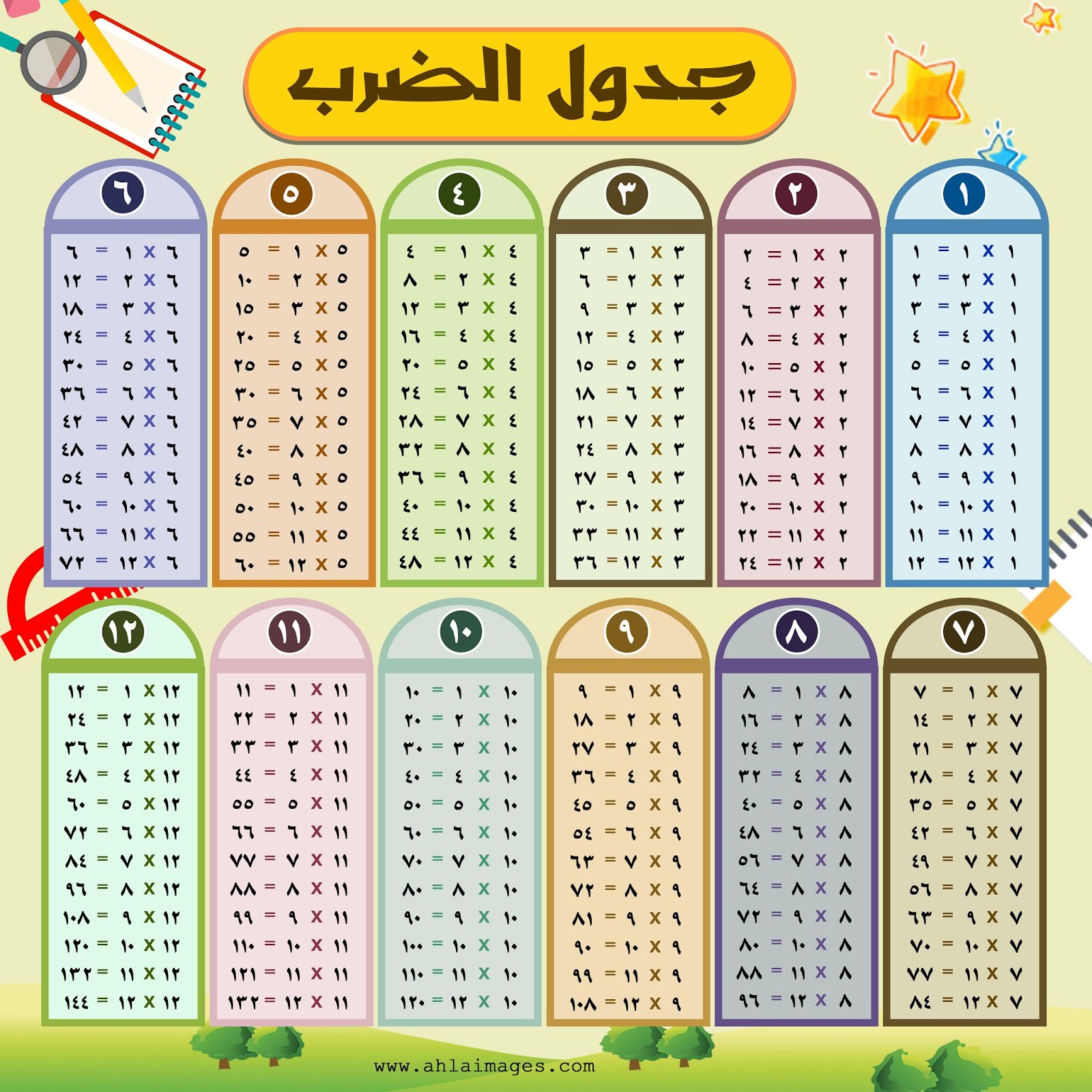
- الضرب العمودي: حيث نضع العاملين فوق بعضهما البعض ونضرب كل رقم في العامل الأول بكل رقم في العامل الثاني، ثم نجمع النتائج جزئيًا.
- الضرب الشبكي: حيث نرسم شبكة وندخل العاملين على الأضلاع الموازية، ثم نضرب كل رقم في كل صف بكل رقم في العمود المقابل، ونضيف النتائج جزئيًا.
- الضرب الذهني: حيث نستخدم حقائق الضرب الأساسية واستراتيجيات الجمع والطرح لت حل المسائل ذهنيا.

الاستراتيجيات الذهنية في الضرب

هناك العديد من الاستراتيجيات الذهنية التي يمكن استخدامها لجعل الضرب أسهل، ومنها:

- التجميع: حيث نقوم بتجميع الأرقام لتسهيل العملية، على سبيل المثال، 25 × 3 = (20 × 3) + (5 × 3)
- التوزيع: حيث نضرب رقمًا واحدًا في العاملين ثم نجمع النتائج، على سبيل المثال، 34 × 5 = (30 × 5) + (4 × 5)
- التخمين والتحقق: حيث نخمن الإجابة ثم نتحقق منها عن طريق الضرب الفعلي، على سبيل المثال، 123 × 4 ≈ 500

تطبيقات عملية للضرب

للضرب تطبيقات عديدة في الحياة العملية، منها:

- إيجاد المساحة: حيث نضرب الطول في العرض لإيجاد مساحة الشكل المستطيل أو المربع.
- إيجاد الحجم: حيث نضرب الطول في العرض في الارتفاع لإيجاد حجم المنشور أو المكعب.
- إيجاد المسافة المقطوعة: حيث نضرب السرعة في الزمن لإيجاد المسافة المقطوعة.

خاتمة مطوية الضرب

في النهاية، فإن الضرب هو عملية أساسية في الرياضيات لها العديد من التطبيقات العملية، ويمكن حل الضرب باستخدام مجموعة متنوعة من الطرق، بما في ذلك الضرب العمودي والشبكي والذهني، وعند إتقان مفهوم الضرب، يمكن للطلاب حل مجموعة واسعة من المسائل الرياضية بحلول دقيقة وفعالة.
