نوع المعدل

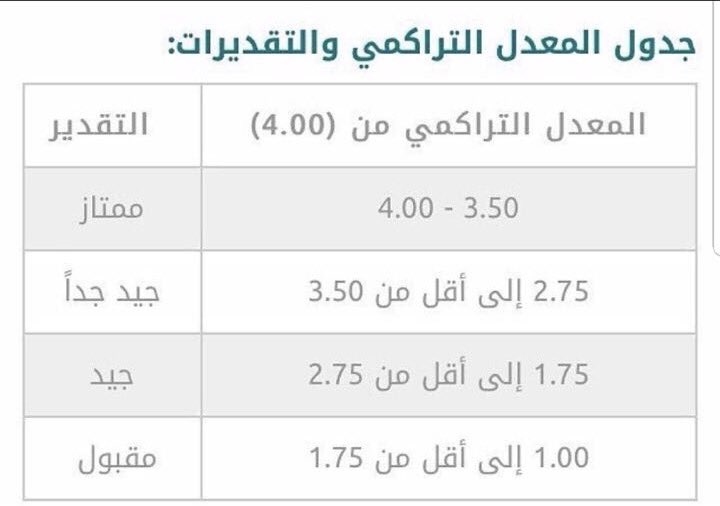
أنواع المعدلات

المعدل هو مقياس إحصائي يُستخدم لوصف مركز توزيع البيانات. هناك أنواع مختلفة من المعدلات، ولكل منها طريقة حساب خاصة به. فيما يلي الأنواع السبعة الأكثر شيوعًا من المعدلات:

1. المتوسط

المتوسط هو الأكثر شيوعًا من أنواع المعدلات. ويُحسب عن طريق جمع جميع القيم في مجموعة البيانات وقسمة المجموع على عدد القيم. المتوسط هو مقياس جيد لمركز توزيع البيانات إذا كانت البيانات متماثلة نسبيًا.

على سبيل المثال، إذا كانت لدينا مجموعة بيانات تحتوي على الأرقام 1، 3، 5، 7، 9، فإن المتوسط سيكون (1 + 3 + 5 + 7 + 9) / 5 = 5.

المتوسط حساس للقيم المتطرفة. إذا كانت مجموعة البيانات تحتوي على قيم عالية أو منخفضة للغاية، فقد يؤثر ذلك على متوسط القيمة. على سبيل المثال، إذا أضفنا القيمة 100 إلى مجموعة البيانات أعلاه، فإن المتوسط سيزيد إلى (1 + 3 + 5 + 7 + 9 + 100) / 6 = 17.

2. الوسيط

الوسيط هو المعدل الثاني الأكثر شيوعًا. ويُحسب عن طريق ترتيب القيم في مجموعة البيانات حسب الترتيب الصاعد وإيجاد القيمة الوسطى. الوسيط هو مقياس جيد لمركز توزيع البيانات إذا كانت البيانات مائلة.

على سبيل المثال، إذا كانت لدينا مجموعة البيانات 1، 3، 5، 7، 9، فإن الوسيط سيكون 5 لأن هذه هي القيمة الوسطى عندما يتم ترتيب القيم بترتيب تصاعدي.

الوسيط غير حساس للقيم المتطرفة. إذا أضفنا القيمة 100 إلى مجموعة البيانات أعلاه، فإن الوسيط سيبقى 5 لأن هذه القيمة ليست القيمة الوسطى عندما يتم ترتيب القيم بترتيب تصاعدي.

3. المنوال

المنوال هو المعدل الذي يظهر كثيرًا في مجموعة البيانات. المنوال هو مقياس جيد لمركز توزيع البيانات إذا كانت البيانات متعددة الوسائط.

على سبيل المثال، إذا كانت لدينا مجموعة البيانات 1، 3، 3، 5، 7، 9، فإن المنوال هو 3 لأن هذه هي القيمة التي تظهر كثيرًا في مجموعة البيانات.

المنوال حساس للقيم المتكررة. إذا أضفنا القيمة 100 إلى مجموعة البيانات أعلاه، فإن المنوال سيصبح 3 و 100 لأن كلتا القيمتين تظهران كثيرًا في مجموعة البيانات.

4. المتوسط المرجح

المتوسط المرجح هو نوع من المتوسط الذي يأخذ في الاعتبار تكرار القيم في مجموعة البيانات. يُحسب المتوسط المرجح عن طريق ضرب كل قيمة في مجموعة البيانات بتكرارها ثم قسمة المجموع على إجمالي التكرارات.

على سبيل المثال، إذا كانت لدينا مجموعة البيانات 1، 3، 3، 5، 7، 9، حيث تظهر القيمة 3 مرتين، فإن المتوسط المرجح سيكون (1 × 1 + 3 × 2 + 5 × 1 + 7 × 1 + 9 × 1) / 6 = 4.

المتوسط المرجح مفيد عندما تكون بعض القيم في مجموعة البيانات أكثر أهمية من غيرها. على سبيل المثال، إذا كانت لدينا مجموعة بيانات تحتوي على درجات الاختبارات لطلاب في فئة، فإن المتوسط المرجح يمكن استخدامه لإيجاد متوسط درجات الطلاب مع مراعاة وزن كل درجة حسب عدد الطلاب الذين حصلوا عليها.

5. متوسط الانحراف المطلق

متوسط الانحراف المطلق هو مقياس للتشتت يُحسب عن طريق حساب متوسط المسافة بين كل قيمة في مجموعة البيانات والمتوسط. متوسط الانحراف المطلق هو مقياس جيد لتشتت البيانات إذا كانت البيانات متماثلة نسبيًا.

على سبيل المثال، إذا كانت لدينا مجموعة البيانات 1، 3، 5، 7، 9، فإن متوسط الانحراف المطلق سيكون ( 1 – 5 + 3 – 5 + 5 – 5 + 7 – 5 + 9 – 5 ) / 5 = 2.

متوسط الانحراف المطلق غير حساس للقيم المتطرفة. إذا أضفنا القيمة 100 إلى مجموعة البيانات أعلاه، فإن متوسط الانحراف المطلق سيزداد إلى ( 1 – 5 + 3 – 5 + 5 – 5 + 7 – 5 + 9 – 5 + 100 – 5 ) / 6 = 21.

6. التباين

التباين هو مقياس للتشتت يُحسب عن طريق حساب متوسط مربع المسافة بين كل قيمة في مجموعة البيانات والمتوسط. التباين هو مقياس جيد لتشتت البيانات إذا كانت البيانات متماثلة نسبيًا.

على سبيل المثال، إذا كانت لدينا مجموعة البيانات 1، 3، 5، 7، 9، فإن التباين سيكون ( 1 – 5 ^2 + 3 – 5 ^2 + 5 – 5 ^2 + 7 – 5 ^2 + 9 – 5 ^2) / 5 = 8.

التباين حساس للقيم المتطرفة. إذا أضفنا القيمة 100 إلى مجموعة البيانات أعلاه، فإن التباين سيزداد إلى ( 1 – 5 ^2 + 3 – 5 ^2 + 5 – 5 ^2 + 7 – 5 ^2 + 9 – 5 ^2 + 100 – 5 ^2) / 6 = 1340.

7. الانحراف المعياري

الانحراف المعياري هو جذر التباين. الانحراف المعياري هو مقياس جيد لتشتت البيانات إذا كانت البيانات متماثلة نسبيًا.

على سبيل المثال، إذا كانت لدينا مجموعة البيانات 1، 3، 5، 7، 9، فإن الانحراف المعياري سيكون √8 = 2.83.

الانحراف المعياري حساس للقيم المتطرفة. إذا أضفنا القيمة 100 إلى مجموعة البيانات أعلاه، فإن الانحراف المعياري سيزداد إلى √1340 = 36.55.

الخلاصة

هناك أنواع مختلفة من المعدلات، ولكل منها طريقة حساب خاصة بها. اختيار المعدل الأنسب لمجموعة بيانات معينة يعتمد على توزيع البيانات. إذا كانت البيانات متماثلة نسبيًا، فإن المتوسط أو الوسيط أو المتوسط المرجح هو خيار جيد. إذا كانت البيانات مائلة، فإن الوسيط هو خيار جيد. إذا كانت البيانات متعددة الوسائط، فإن المنوال هو خيار جيد. إذا كانت بعض القيم في مجموعة البيانات أكثر أهمية من غيرها، فإن المتوسط المرجح هو خيار جيد. إذا كنت مهتمًا بتشتت البيانات، فإن متوسط الانحراف المطلق والتباين والانحراف المعياري هي خيارات جيدة.