خريطة مفاهيم المثلثات المتطابقة

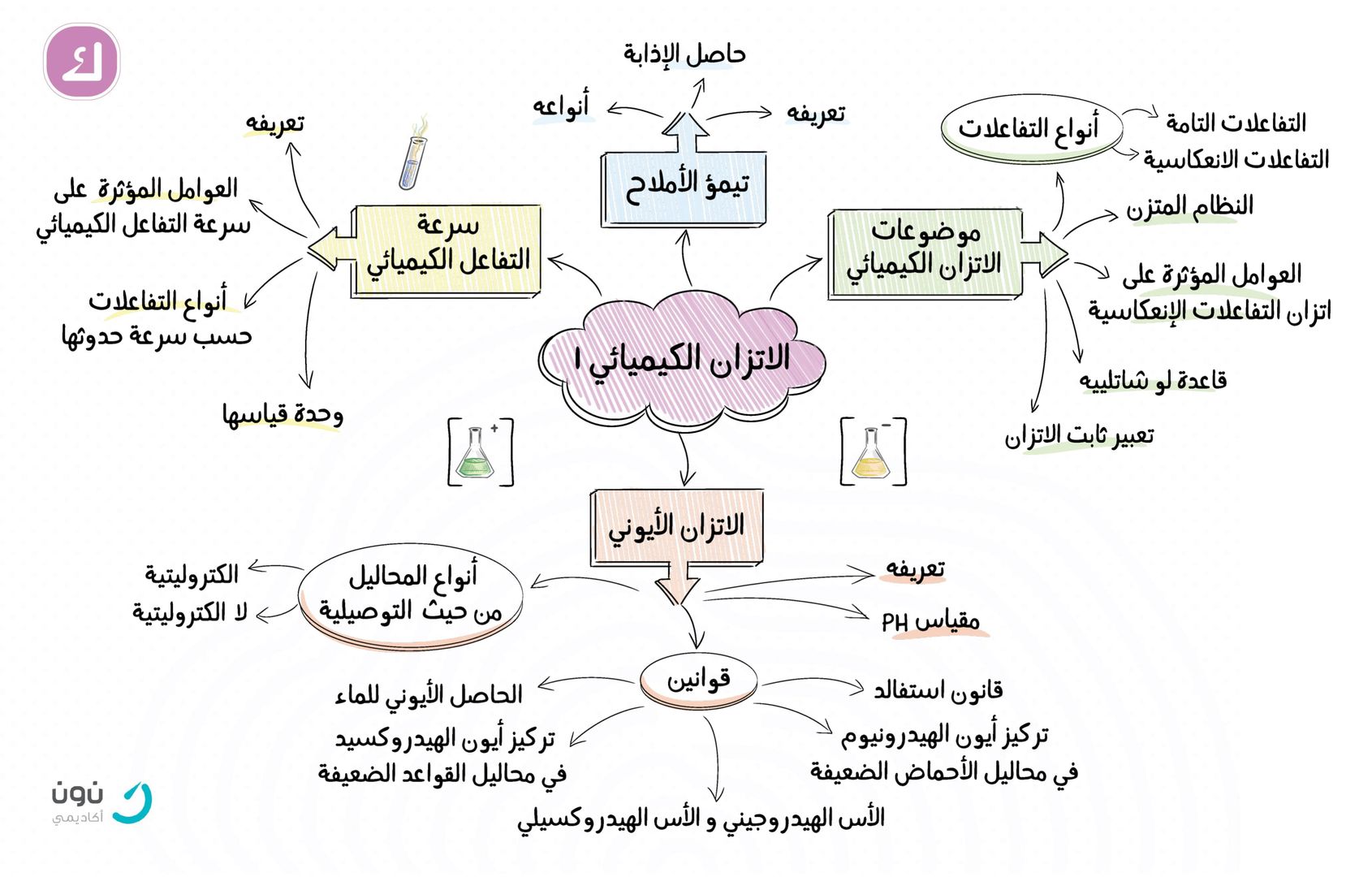
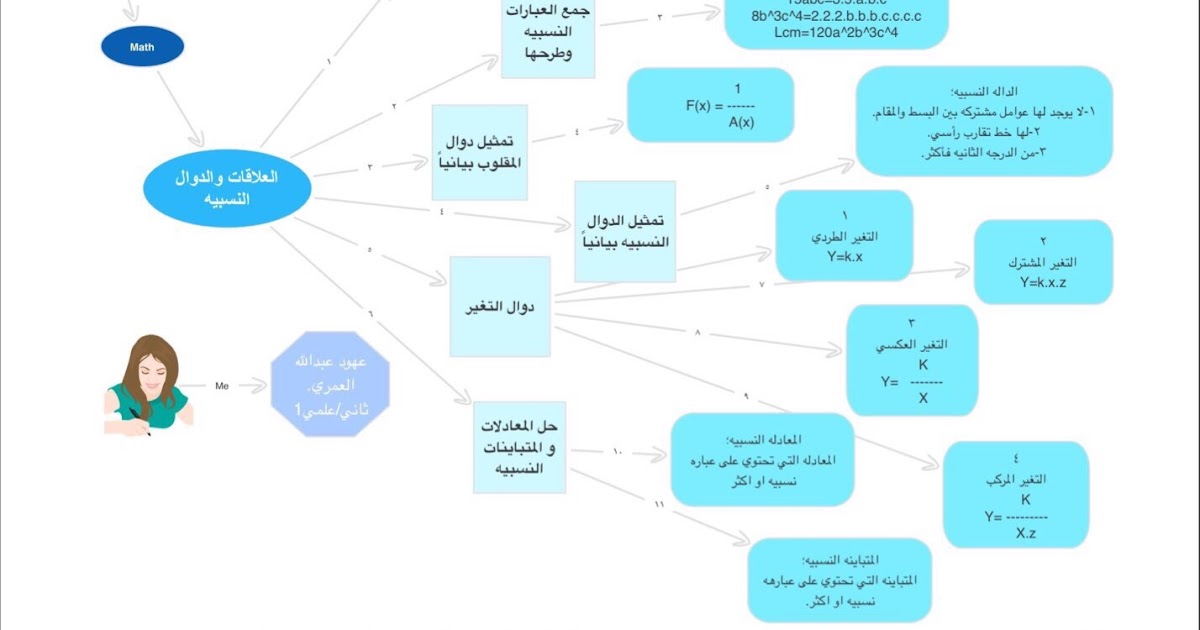
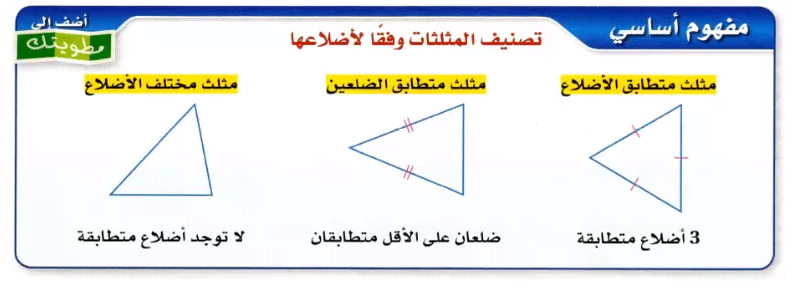
خريطة مفاهيم المثلثات المتطابقة

في الهندسة، تكون المثلثات المتطابقة ثلاث مثلثات لها نفس الشكل والحجم. وهذا يعني أن جميع أضلاعها وزواياها متساوية. يمكن إثبات تطابق المثلثات باستخدام مجموعة من النظريات المعروفة باسم معايير التطابق. يوجد خمس معايير تطابق للمثلثات، والتي يتم اختصارها عادةً باسم SSS ، SAS ، ASA ، AAS و-HL.

SSS (الضلع-الضلع-الضلع)

وفقًا لمعيار SSS، فإن المثلثات متطابقة إذا كانت أضلاعها الثلاثة متساوية. على سبيل المثال، إذا كان لدينا مثلثان لهما أضلاع (أ، ب، ج) و (د، هـ، و)، فإن المثلثين متطابقان إذا كانت أ=د، ب=هـ، ج=و.

هذا لأن أطوال الأضلاع تحدد بشكل فريد شكل وحجم المثلث. وبالتالي، إذا كانت جميع أضلاع مثلثين متساوية، فيجب أن يكون المثلثان متطابقين.

يمكن استخدام معيار SSS لإثبات تطابق المثلثات في مجموعة متنوعة من التطبيقات، مثل إيجاد قياسات الزوايا المفقودة أو تحديد ما إذا كانت المثلثات متشابهة.

SAS (الضلع-الزاوية-الضلع)

وفقًا لمعيار SAS، فإن المثلثات متطابقة إذا كان لها ضلعان متطابقان وزاوية واحدة بينهما متساوية. على سبيل المثال، إذا كان لدينا مثلثان لهما أضلاع (أ، ب، ج) و (د، هـ، و) وزوايا (ألفا، بيتا، جاما) و (دلتا، إبسيلون، زتا)، فإن المثلثين متطابقين إذا كانت أ=د، ب=هـ، ألفا=دلتا.

هذا لأن الضلعين المتطابقين والزاوية الواقعة بينهما تحددان بشكل فريد شكل المثلث. وبالتالي، إذا كان ضلعان وزاوية بينهما في مثلثين متطابقين، فيجب أن يكون المثلثان متطابقين.

يمكن استخدام معيار SAS لإثبات تطابق المثلثات في مجموعة متنوعة من التطبيقات، مثل إيجاد قياسات الزوايا المفقودة أو تحديد ما إذا كانت المثلثات متشابهة.

ASA (الزاوية-الضلع-الزاوية)

وفقًا لمعيار ASA، فإن المثلثات متطابقة إذا كانت لها زاويتان متطابقتان وضلع واحد متطابق بينهما. على سبيل المثال، إذا كان لدينا مثلثان لهما أضلاع (أ، ب، ج) و (د، هـ، و) وزوايا (ألفا، بيتا، جاما) و (دلتا، إبسيلون، زتا)، فإن المثلثين متطابقين إذا كانت ألفا=دلتا، بيتا=إبسيلون، ج=و.

هذا لأن الزاويتين المتطابقتين والضلع الواصل بينهما تحددان بشكل فريد شكل المثلث. وبالتالي، إذا كانت زاويتان وضلع بينهما في مثلثين متطابقين، فيجب أن يكون المثلثان متطابقين.

يمكن استخدام معيار ASA لإثبات تطابق المثلثات في مجموعة متنوعة من التطبيقات، مثل إيجاد قياسات الأضلاع المفقودة أو تحديد ما إذا كانت المثلثات متشابهة.

AAS (الزاوية-الزاوية-الضلع)

وفقًا لمعيار AAS، فإن المثلثات متطابقة إذا كانت لها زاويتان متطابقتان وضلع غير متجاور متطابق. على سبيل المثال، إذا كان لدينا مثلثين لهما أضلاع (أ، ب، ج) و (د، هـ، و) وزوايا (ألفا، بيتا، جاما) و (دلتا، إبسيلون، زتا)، فإن المثلثين متطابقين إذا كانت ألفا=دلتا، بيتا=إبسيلون، ب=هـ.

هذا لأن الزاويتين المتطابقتين والضلع غير المتجاور بينهما تحددان بشكل فريد شكل المثلث. وبالتالي، إذا كانت زاويتان وضلع غير متجاور بينهما في مثلثين متطابقين، فيجب أن يكون المثلثان متطابقين.

يمكن استخدام معيار AAS لإثبات تطابق المثلثات في مجموعة متنوعة من التطبيقات، مثل إيجاد قياسات الزوايا المفقودة أو تحديد ما إذا كانت المثلثات متشابهة.

HL (الضلع-الزاوية-الضلع)

وفقًا لمعيار HL، فإن المثلثات متطابقة إذا كان لها ضلعان متطابقان وزاوية متضمنة متساوية. على سبيل المثال، إذا كان لدينا مثلثان لهما أضلاع (أ، ب، ج) و (د، هـ، و) وزوايا (ألفا، بيتا، جاما) و (دلتا، إبسيلون، زتا)، فإن المثلثين متطابقين إذا كانت أ=د، ب=هـ، جاما=زتا.

هذا لأن الضلعين المتطابقين والزاوية المتضمنة تحددان بشكل فريد شكل المثلث. وبالتالي، إذا كان ضلعان وزاوية متضمنة في مثلثين متطابقين، فيجب أن يكون المثلثان متطابقين.

يمكن استخدام معيار HL لإثبات تطابق المثلثات في مجموعة متنوعة من التطبيقات، مثل إيجاد قياسات الزوايا المفقودة أو تحديد ما إذا كانت المثلثات متشابهة.

الاختبار بزوايا قائمة

إذا كان للمثلثين زاويتان قائمتان، فإن المثلثين متطابقان.

لإثبات ذلك، نفترض أن لدينا مثلثين قائمين الزاوية، أحدهما له زاويتان قائمتان عند أ وب، والآخر له زاويتان قائمتان عند ج ود. نظرًا لأن مجموع الزوايا الداخلية للمثلث هو 180 درجة، فإن لدينا:

أ + ب + 90 = 180
ج + د + 90 = 180

بطرح المعادلة الأولى من المعادلة الثانية، نحصل على:

د – ب = 0
د = ب

وبالتالي، فإن للمثلثين ضلعين متطابقين ومضمونة متساوية. وبالتالي، وفقًا لمعيار SAS، فإن المثلثين متطابقان.

الاختبار بالتراكب

إذا كان يمكن لواحد من المثلثين أن يتراكب تمامًا فوق الآخر، فإن المثلثين متطابقان.

لإثبات ذلك، نفترض أن لدينا مثلثين ABC و XYZ بحيث يمكن لـ ABC أن يتراكب تمامًا فوق XYZ. هذا يعني أن قمة A تتطابق مع قمة X، والقمة B تتطابق مع القمة Y، والقمة C تتطابق مع القمة Z.

نظرًا لأن المثلثين متراكبين، فإن جميع أضلاعهما وزواياه متطابقة. وبالتالي، فإن المثلثين متطابقان.

استنتاج

خريطة مفاهيم المثلثات المتطابقة هي أداة قوية لإثبات تطابق المثلثات. توفر معايير التطابق الخمسة (SSS، SAS، ASA، AAS، HL) بالإضافة إلى اختبارين إضافيين (الاختبار بزوايا قائمة والاختبار بالتراكب) طرقًا مختلفة لإثبات أن المثلثين متطابقين. يمكن استخدام هذه المعايير لحل مجموعة متنوعة من المشاكل الهندسية، مثل إيجاد قياسات الزوايا المفقودة أو تحديد ما إذا كانت المثلثات متشابهة.