خريطة مفاهيم التوابع

مقدمة
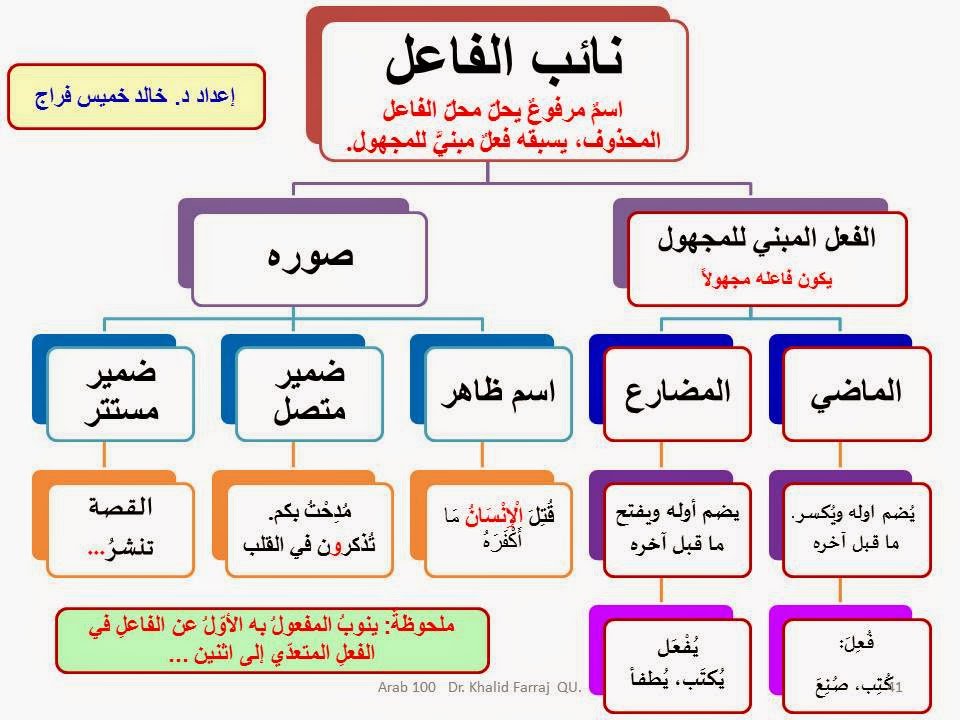
التابع هو علاقة بين متغيرين، حيث لكل قيمة للمتغير الأول (المدخل) قيمة واحدة أو أكثر للمتغير الثاني (المخرج). ويمكن تمثيل التابع بيانيًا على شكل منحنى أو خط، أو جبريًا على شكل معادلة. وتصنف التوابع إلى أنواع عديدة، لكل نوع خصائصه وعملياته الخاصة.

أنواع التوابع
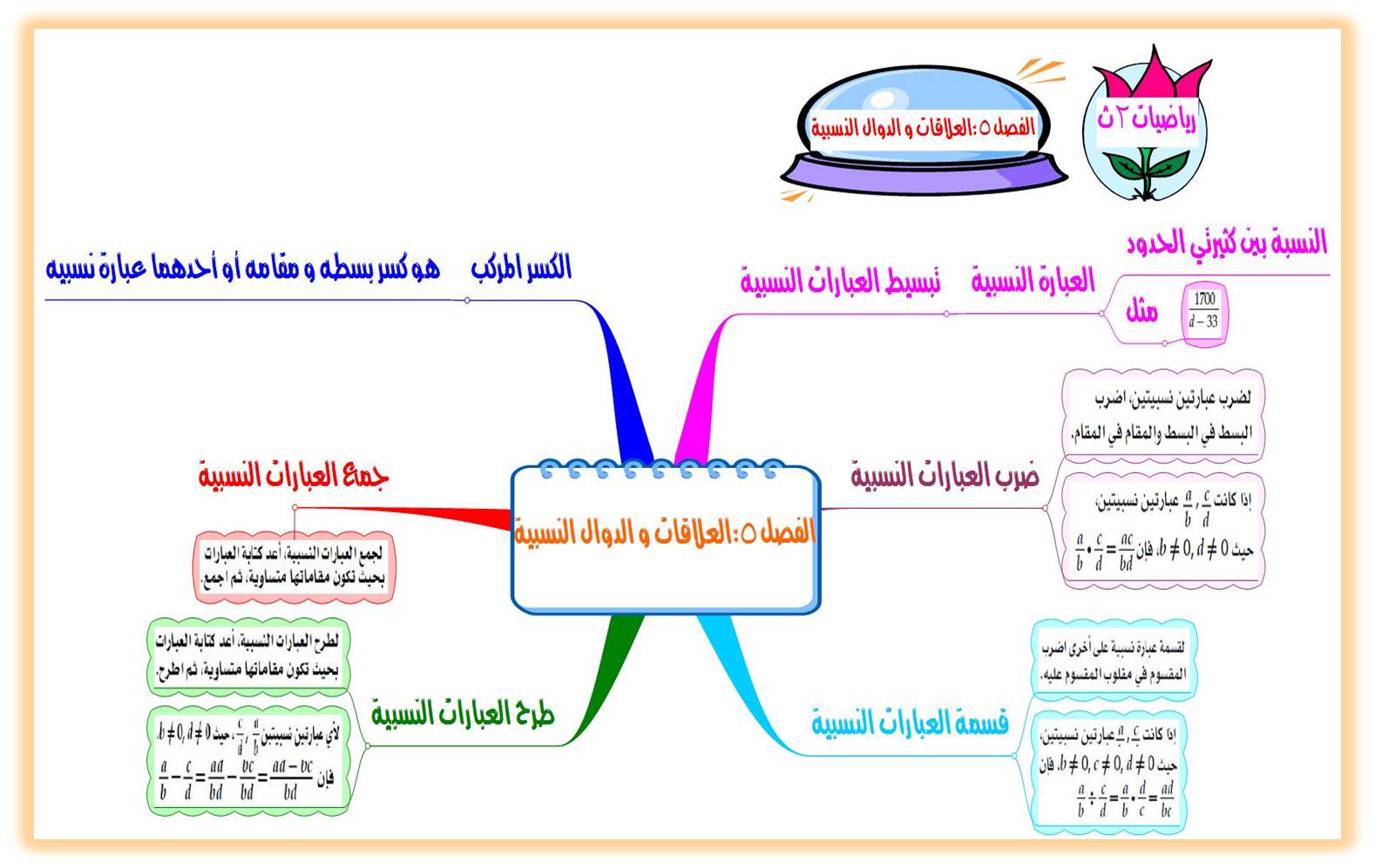

التوابع الخطية
هي توابع لها معدل تغير ثابت، وتمثلها معادلات خطية من الشكل y = mx + b. وتمتلك التوابع الخطية ميل ثابت، يحدد معدل تغيرها، كما أنها تمر بنقطة ثابتة على المحور الصادي، يحددها ثابت البعد.
التوابع التربيعية
هي توابع لها معدل تغير متغير، وتمثلها معادلات تربيعية من الشكل y = ax2 + bx + c. وتمتلك التوابع التربيعية قمة أو نقطة دنيا، تحددها قيمة متغير معين. كما أنها يمكن أن يكون لها جذران حقيقيان أو مركبان.

التوابع الكسرية
هي توابع لها نطاق محدد، وتمثلها معادلات كسرية من الشكل y = p(x) / q(x). وتمتلك التوابع الكسرية خطوطًا مقاربة أفقية أو رأسية، تحدد سلوكها عند النهايات. كما أنها يمكن أن يكون لها نقاط عدم استمرارية أو نقاط مقاربة غير محدودة.

التوابع الأسية
هي توابع لها أساس ثابت، وتمثلها معادلات أسية من الشكل y = a^x. وتمتلك التوابع الأسية معدل نمو أو اضمحلال ثابت، يحدده الأس. كما أنها تمر بنقطة ثابتة على المحور الصادي، وهي نقطة الأصل.

التوابع اللوغاريتمية
هي توابع هي عكس التوابع الأسية، وتمثلها معادلات لوغاريتمية من الشكل y = log(x). وتمتلك التوابع اللوغاريتمية معدل نمو أو اضمحلال غير ثابت، يحدده الأساس. كما أنها تمر بنقطة ثابتة على المحور السيني، وهي النقطة (1, 0).
التوابع الدورية

هي توابع تتكرر قيمها بعد فترة زمنية أو زاوية معينة، وتمثلها معادلات دورية من الشكل y = f(x + P). وتمتلك التوابع الدورية فترة ثابتة، تحدد تكرارها، كما أنها يمكن أن تكون دوال جيب أو جيب تمام أو ظل أو ظل تمام.
التوابع المتسامية
هي توابع لا يمكن تمثيلها بمتعددات حدود أو دوال جبرية، وتمثلها معادلات متسامية من الشكل y = e^x أو y = sin(x). وتمتلك التوابع المتسامية خصائص فريدة، مثل عدم وجود مشتق دائم أو انتگرال ابتدائي.

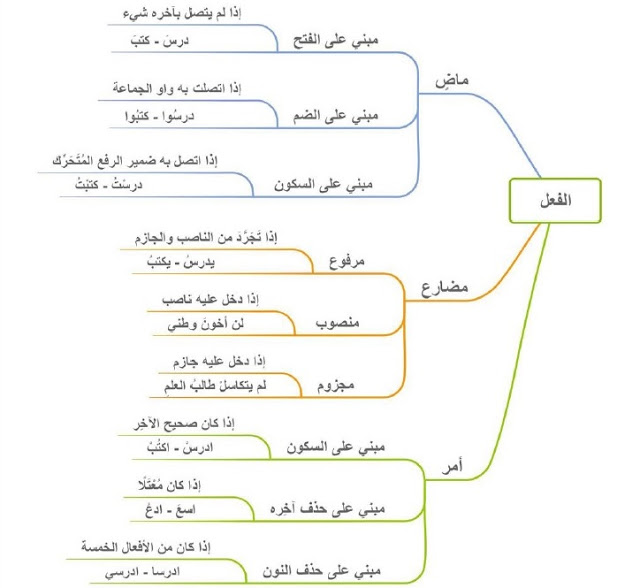
خصائص التوابع

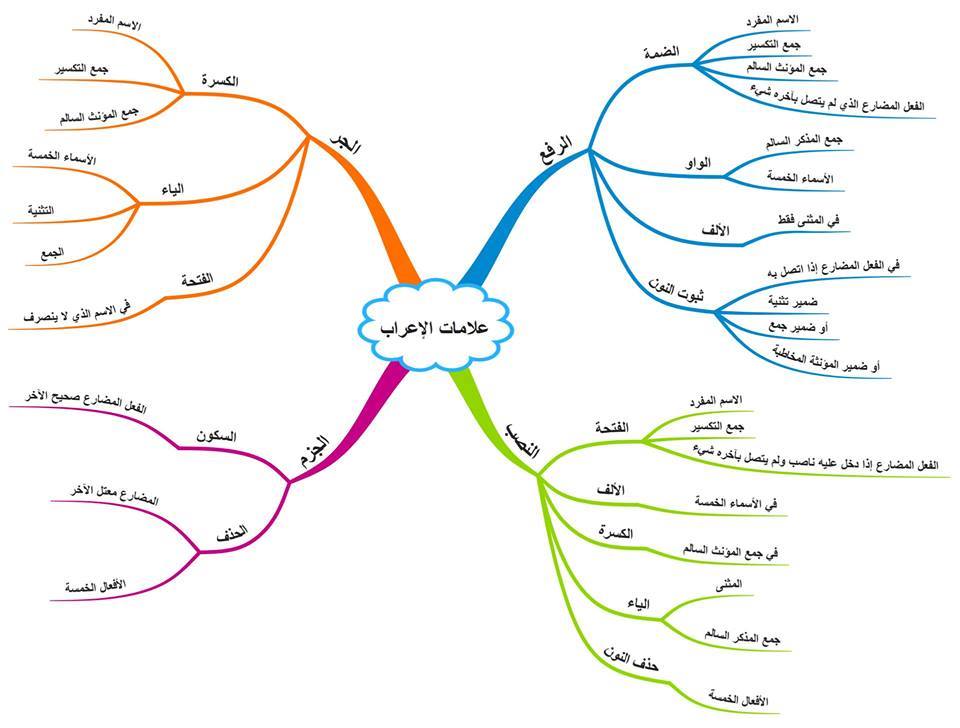
مجال التابع
هو مجموعة القيم التي يمكن أن يأخذها المتغير المستقل.
مدى التابع

هو مجموعة القيم التي يمكن أن يأخذها المتغير التابع.
دالة التابع
هي العلاقة بين المدخل والمخرج في التابع.
زيادة التابع

يقال إن التابع متزايد إذا كانت قيمته تزداد مع زيادة قيم المتغير المستقل.
نقصان التابع
يقال إن التابع متناقص إذا كانت قيمته تقل مع زيادة قيم المتغير المستقل.
ثبات التابع
يقال إن التابع ثابت إذا كانت قيمته لا تتغير مع تغير قيم المتغير المستقل.
دالة التابع العكسية
هي دالة عكسية لدالة معينة، حيث يمكن استبدالها بالدالة الأصلية لتحصل على المتغير المستقل.
تطبيقات التوابع

تستخدم التوابع في العديد من المجالات، منها:

العلوم الطبيعية
تستخدم التوابع لوصف وتوقع الظواهر الطبيعية، مثل نمو السكان أو تحلل المواد.

العلوم الاجتماعية

تستخدم التوابع لتحليل البيانات الاقتصادية والاجتماعية، مثل التنبؤ بالنمو الاقتصادي أو معدلات البطالة.
التكنولوجيا
تستخدم التوابع في تصميم الدوائر الإلكترونية والبرمجيات وأنظمة التحكم.

الرياضيات

تستخدم التوابع في حل المعادلات والمتباينات وإثبات النظريات.
خاتمة
التوابع هي أدوات رياضية قوية تستخدم لتمثيل العلاقات بين المتغيرات وتحلل البيانات وحل المشاكل. وتصنف التوابع إلى أنواع مختلفة، لكل نوع خصائصه وعملياته الخاصة. ومن خلال فهم أنواع وخصائص التوابع، يمكن استخدامها بشكل فعال في مجموعة واسعة من التطبيقات.