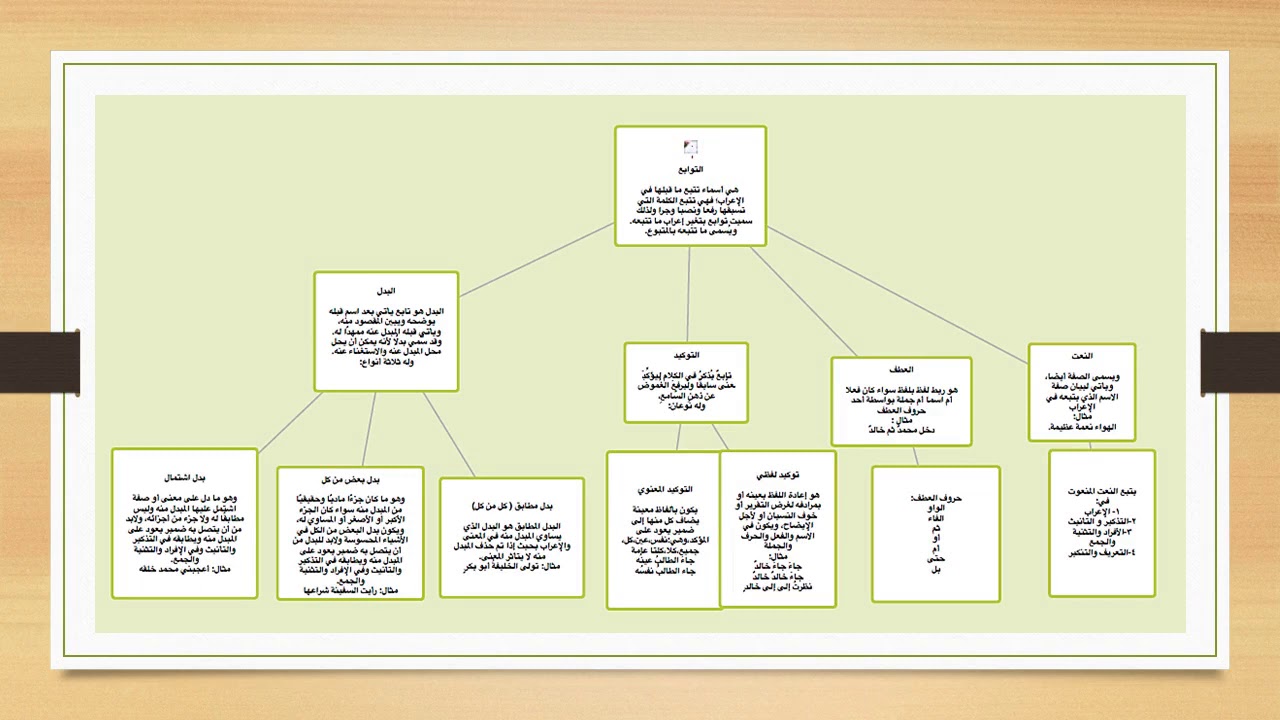
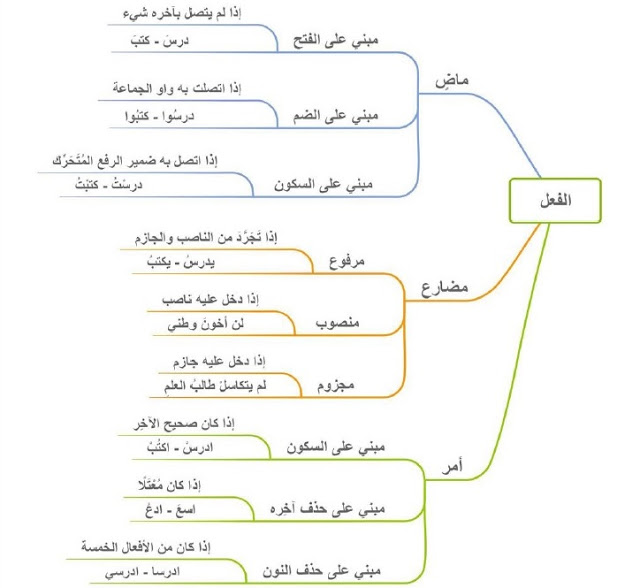
خريطة مفاهيم التوابع

مجالات التوابع

مجال التابع هو مجموعة جميع قيم المتغير المستقل المسموح بها. يعتمد مجال التابع على القيود المفروضة على دالة التابع.


يمكن أن تكون مجالات التوابع مجموعات مختلفة من الأرقام، مثل الأعداد الحقيقية أو الأعداد المركبة.
مدى التوابع

مدى التابع هو مجموعة جميع قيم المتغير التابع التي يمكن أن يأخذها التابع. يعتمد مدى التابع على مجال التابع ودالة التابع.

يمكن أن تكون مداخل التوابع مجموعات مختلفة من الأرقام، مثل الأعداد الحقيقية أو الأعداد المركبة أو الأشياء الأخرى مثل المتجهات أو المصفوفات.
أنواع التوابع
هناك أنواع مختلفة من التوابع، لكل منها خصائصها الفريدة. بعض أنواع التوابع الشائعة تشمل:
– التوابع الخطية: هذه التوابع لها معادلات من الشكل y = mx + b، حيث m و b ثابتان.
– التوابع التربيعية: هذه التوابع لها معادلات من الشكل y = ax^2 + bx + c، حيث a و b و c ثابتات.
– التوابع الكسرية: هذه التوابع لها معادلات من الشكل y = a/x، حيث a ثابت.
– التوابع الجذرية: هذه التوابع لها معادلات من الشكل y = √x، حيث a ثابت.
– التوابع الأسية: هذه التوابع لها معادلات من الشكل y = a^x، حيث a ثابت.
– التوابع اللوغاريتمية: هذه التوابع لها معادلات من الشكل y = log(x)، حيث a ثابت.

– التوابع المثلثية: هذه التوابع هي توابع دورية لها معادلات من الشكل y = sin(x) أو y = cos(x) أو y = tan(x).

تمثيل التوابع

يمكن تمثيل التوابع بيانيًا أو جبرًا. التمثيل البياني لتابع هو رسم بياني يمثل العلاقة بين المتغير المستقل والمتغير التابع.
التعبير الجبري عن تابع هو معادلة رياضية تصف العلاقة بين المتغير المستقل والمتابع التابع.

خصائص التوابع
للتوابع خصائص مختلفة يمكن استخدامها لوصف سلوكها. بعض خصائص التوابع الشائعة تشمل:
– الدورية: التوابع الدورية هي توابع تتكرر قيمها بعد فترة زمنية منتظمة.

– التناظر: التوابع المتناظرة لها مخططات بيانية متناظرة حول محور الإحداثيات أو خط العمودي.

– القيم القصوى: القيم القصوى للتابع هي أكبر وأصغر قيم يمكن أن يأخذها التابع.
– القيم الدنيا: القيم الدنيا للتابع هي أكبر وأصغر قيم يمكن أن يأخذها التابع.

– النقاط الحرجة: النقاط الحرجة للتابع هي النقاط التي يكون فيها التابع غير قابل للاشتقاق أو ميل التابع يساوي صفرًا.

– القيم العرضية: القيم العرضية للتابع هي قيم التابع عند نقاط معينة.
– القيم المتطرفة: القيم المتطرفة للتابع هي أكبر وأصغر قيم يمكن أن يأخذها التابع في مجال التابع.

تطبيقات التوابع
للتوابع مجموعة واسعة من التطبيقات في مجالات مختلفة مثل:
– العلوم: تستخدم التوابع لنمذجة الظواهر الطبيعية، مثل حركة الأجسام أو نمو السكان.
– الهندسة: تستخدم التوابع لتصميم الهياكل وحساب المساحات والحجوم.

– الأعمال: تستخدم التوابع لنمذجة السلوك الاقتصادي، مثل العرض والطلب.

خريطة مفاهيم التوابع هي أداة قيمة لتنظيم وفهم المفاهيم المختلفة المتعلقة بالتوابع. من خلال فهم المفاهيم الأساسية المتعلقة بالمجالات والمدى والأنواع والتمثيل والخصائص والتطبيقات، يمكن للمرء اكتساب تقدير كامل لقوة التوابع وأهميتها في مختلف المجالات.